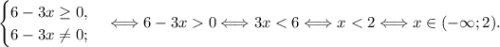Быстро, ! найти область определения
Другие вопросы по теме Алгебра
Популярные вопросы
- решить задачу по геометрии(найти сторону треугольника) 10-11 класс...
1 - 1.Назовите основные свойства живой природы 2.Приведите примеры многообразия...
3 - Обязательно с решение с 12 по 20 и еще с пункта вычисли или у и...
1 - Враженя від пісні червона рута піду в далекі гори та інші які співав...
1 - Еволюція образу кріпака в повісті інститутка...
2 - Знайдіть суму перших шести членів геометричної прогресії, перший...
3 - Какие человеческие проявления автор романа «Война и мир» считал...
3 - Положение Таиланда относительно крупных форм рельефа....
2 - очень в скобках написал во на русском! Imagine your travel to the...
2 - 2-й раз, Выполнить седьмое задание....
3
Для большого множества функций область определения - всё R.
Область определения ограничивается при:1) делении на выражение, содержащее x;
Знаменатель не может быть равен нулю!
2) наличии корня чётной степени, содержащего x.
Подкоренное значение неотрицательно!
Перейдём непосредственно к вопросу.1) Деления или корня нет ⇒ x ∈ R.
2)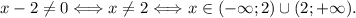
3)