Bn - прогрессия, b4-b1=78, b1+b2+b3=39. найдите b1 и q
Другие вопросы по теме Алгебра
Популярные вопросы
- It s the _. The energy comes from_ Английский...
1 - 2. С целью выявления в содержании “Временных правил” колонизационных...
2 - Кроссворд на тему чередующиеся гласные в корне 10 слов с вопросами...
3 - Центральная Россия Задания 1. Обозначьте границы региона, подпишите...
1 - 17а^2-34ax+17x^2,якщо а=3,7 і х=2,7...
3 - Чому одні країни пішли демократичним шляхом , а інші відмовились...
3 - Скласти 2 питання кожного пункту параграфу Господарство та повсякденне...
1 - #15 Найдите сумму всех различных значений функции f (x) = x² -...
1 - Хечким ва хечнарса унутилмайди эссе...
3 - С каждым словарным словом составить словосочетание, орфограммы...
3
Вспомним, как можно подать любой член г.п.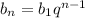
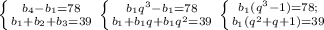
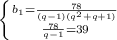
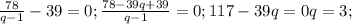 (входит в одз)
(входит в одз)
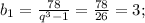
Запишем систему уравнений:
ответ: b1=3 q=3;