1. Алгебра
  2. Arctgx=arcsin(x/sqrt(1+x^2)) нужно

Arctgx=arcsin(x/sqrt(1+x^2))
нужно доказать люди добрые

lpam lpam    1   04.12.2020 18:55    4

Ответы
Шаров2005 Шаров2005  03.01.2021 19:05

Введем замену: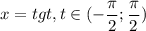 x=tgt, t\in (-\dfrac{\pi}{2};\dfrac{\pi}{2}) . Отметим, что область определения исходного выражения - все действительные числа, и при этом множество значений 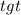tgt на интервале 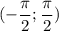(-\dfrac{\pi}{2};\dfrac{\pi}{2}), очевидно, также все действительные числа. А значит полученное после замены выражение равносильно исходному

arctg(tgt)=arcsin\dfrac{tgt}{\sqrt{1+tg^2t}}\\ t=arcsin\dfrac{|cost|tgt}{\sqrt{cos^2t+sin^2t}}\\ t=arcsin\dfrac{cost\cdot tgt}{1}\\ t=arcsin(sin t)\\ t=t

- верно

Ч.т.д.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Ayka557 Ayka557  01.03.2021 17:55
Упростить выражение 1) 7√6-2√54+√96;2) (√80-√20)√5;3) (√10-1)²;4) (6√3+√2)(6√3-√2).​...
anel1985 anel1985  01.03.2021 17:55
РЕШИТЕ 28.12. a) (a: + 36)2;6) (4x2 – 3c)?;B) (5m2 + 3n2)2;r) (6p2 – 8g)​...
olga180982 olga180982  01.03.2021 17:55
2. Число решений системы уравнений Список заданий Условие задания: 10 Б. Сколько решений имеет система уравнений y = 8х +1 y = -33 +4 (В окошке запиши число или «нет решений»,...
КРИЛЛ2000 КРИЛЛ2000  01.03.2021 17:56
Мяч брошен вертикально вверх. Зависимость расстояния h( в метрах) от мяча до земли от времени полета t ( в секундах) выражается формулой h = −4t 2 + 16t ( чертить параболу не...
America555 America555  01.03.2021 17:57
1. Дана функция у= - х2 – 4х+5. a) Запишите координаты вершины параболы. б) Найдите ось симметрии параболы. в) Определите точки пересечения графика с осями координат. г) Постройте...
lizamalaya2012 lizamalaya2012  01.03.2021 17:57
Реши систему уравнений: Szty + = 15 + : 99 ту x — у 5 8 І — у ООО У = (Дробь в ответе должна быть сокращённой)....
Matildos2017 Matildos2017  01.03.2021 17:57
Нужны короткие ответы на воприсы: Как определяется скалярное произведение векторов, заданных своими координатами? 28. Как определяется модуль вектора, заданного своими координатами?...
lizench lizench  28.10.2020 12:19
Найдите множество точек координатной плоскости, которое задано системой неравенств очень нужен график...
ЕвгешаК2003 ЕвгешаК2003  28.10.2020 12:19
Теңдеуді шешіндер(x+4)(x-3)-(x-5)(x+2)=6​...
Lobaneckste Lobaneckste  28.10.2020 12:18
Функция задана формулой у = 4х + 18 Определите:а) значение у, если х = 1,5;б) значение х, при котором у = 1.2;в) проходит ли график функции через точку А (–2; 7).2. а) Постройте...

Популярные вопросы