АЛГЕБРА, ЛОГАРИФМЫ
установите знак выражения:
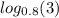
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите периметр прямоугольника сторона которого 12см, а площадь...
2 - Розкладіть на множники та обчисліть 45^2 – 15^2 ...
1 - 1.Ввести масив дійсних чисел розміром n, n вводитися з клавіатури....
3 - Распределите эти товары по странам в которых они производились книги...
2 - 15.Розкрийте значення символів стилет, стилос, булава, Батурин з...
2 - А) разноть чисел 45 и 45 умножить на честное чисел 72 и...
3 - Отгадай загадку. В лес зашёл на 3-х ногах, а вышел на 4-х...
2 - В В игре по перетягиванию каната участвует 4 человека. Два их них...
1 - Решить неравенство y`(x) ,если y=23*x^2+3*23*x-5*23...
3 - Найдите координаты точек пересечения с осью ОУ прямых, являющихся...
2
1. Свойство логарифма относительно возведения в степень:
log_a(x^m) = m * log_a(x), где a - основание логарифма, x - аргумент логарифма, m - показатель степени.
2. Свойство логарифма относительно умножения:
log_a(x * y) = log_a(x) + log_a(y), где a, x и y - аргумент логарифма.
3. Свойство логарифма относительно деления:
log_a(x / y) = log_a(x) - log_a(y), где a, x и y - аргумент логарифма.
4. Свойство замены основания логарифма:
log_a(x) = log_b(x) / log_b(a), где a и b - основания логарифмов, x - аргумент логарифма.
5. Логарифм от числа, равного основанию возводимое в нулевую степень, равен 1:
log_a(a^0) = 1.
Теперь рассмотрим заданное выражение: log_{0.8}(3).
Для определения знака выражения, мы должны учесть несколько факторов.
Первым из них является основание логарифма (0.8). Основание логарифма должно быть положительным числом, и не равным нулю или единице. В данном случае, 0.8 удовлетворяет условию, так как оно положительно и не равно ни нулю, ни единице.
Вторым фактором является аргумент логарифма (3). Аргумент логарифма должен быть положительным числом. В данном случае, аргумент логарифма (3) также удовлетворяет условию, так как он положительный.
Следовательно, основание и аргумент логарифма удовлетворяют условиям, и мы можем продолжить с расчетом этого выражения.
Для нахождения значения данного выражения, мы можем использовать свойство замены основания логарифма, описанное выше.
log_{0.8}(3) = log(3) / log(0.8)
Теперь необходимо вычислить значения обоих логарифмов в числовой форме, прежде чем объединить их с помощью деления.
Чтобы вычислить значения обоих логарифмов, мы можем использовать калькулятор или математическое программное обеспечение. Другой вариант - использовать таблицы логарифмов.
log(3) ≈ 0.4771 (округленное значение)
log(0.8) ≈ -0.0969 (округленное значение)
Теперь мы можем объединить значения обоих логарифмов с помощью деления.
log_{0.8}(3) = log(3) / log(0.8) ≈ 0.4771 / (-0.0969) ≈ -4.9189
Таким образом, знак выражения log_{0.8}(3) - отрицательный.