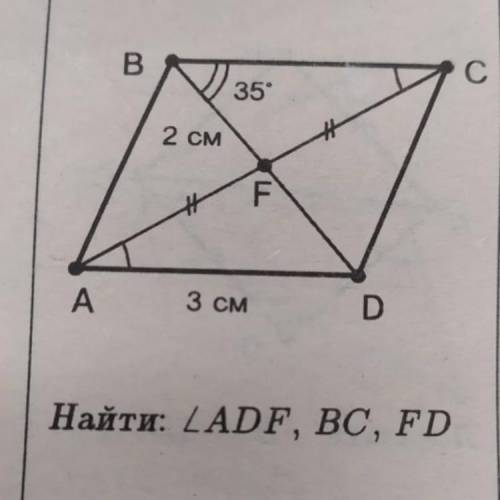
Abcd параллелограмм, угол b=35 градусов, bf=2 см, ad=3см
найти угол adf,bc, fd

Для решения этой задачи, нам понадобятся знания о свойствах параллелограмма и тригонометрии.

Свойства параллелограмма:
1. Противоположные стороны параллелограмма равны и параллельны.
2. Противоположные углы параллелограмма равны.

Итак, обратимся к задаче.

Мы знаем, что угол b (угол между сторонами аb и bc) равен 35 градусам. По свойству 2 параллелограмма, угол a (угол между сторонами ad и ab) также равен 35 градусам.

Нам также известны длины сторон bf (2 см) и ad (3 см).

Для нахождения угла adf, мы можем воспользоваться теоремой косинусов.

Теорема косинусов гласит:
в любом треугольнике, длина одной из сторон в квадрате равна сумме квадратов длин остальных двух сторон минус произведение этих двух сторон на косинус угла между ними.

Мы имеем треугольник adf со сторонами ad (3 см), df (x) и af (2 см).
Таким образом, по теореме косинусов, мы можем получить следующее уравнение:

ad^2 = af^2 + df^2 - 2 * af * df * cos(adf)

Подставляя известные значения:
3^2 = 2^2 + x^2 - 2 * 2 * x * cos(adf)

9 = 4 + x^2 - 4x * cos(adf)

Раскрываем скобки и упрощаем:

5 = x^2 - 4x * cos(adf)

Переносим все члены в левую часть уравнения:

x^2 - 4x * cos(adf) - 5 = 0

Для решения этого уравнения, нам нужно знать значение cos(adf). Однако, у нас этого значения нет. Поэтому, мы не можем найти угол adf точно. Мы можем только приближенно оценить его значение.

Теперь рассмотрим нахождение угла bc.

Угол bc (угол между сторонами bc и cd) равен углу a, так как они являются противоположными углами параллелограмма.
Таким образом, угол bc равен 35 градусам.

Наконец, рассмотрим нахождение угла fd.

Угол fd (угол между сторонами fd и dc) также равен углу b, так как они являются противоположными углами параллелограмма.
Таким образом, угол fd равен 35 градусам.

В результате:
угол adf: не может быть точно найден без известного значения cos(adf)
угол bc: 35 градусов
угол fd: 35 градусов