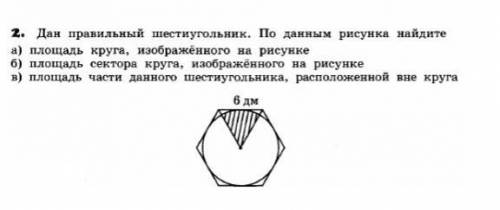
9 класс. алгебра.Дан правильный шестиугольник найдите по рисункам.а) площадь круга, изображенного на рисунке.б)площадт сектора круга. изображенного еа рисунке. в)площадь части даеного шестиугольника расположенного вне кругц

Для решения этой задачи, нам понадобятся знания о формулах, связанных с площадью круга и площадью сектора. Давайте решим задачу по пунктам:

а) Для нахождения площади круга, нам необходимо знать радиус круга. Если мы внимательно посмотрим на рисунок, мы увидим, что радиус круга является стороной шестиугольника. Для расчета площади круга, мы используем формулу: S=πr^2, где S - площадь круга, π - математическая константа, равная примерно 3,14, r - радиус круга.
Так как шестиугольник является правильным, все его стороны и радиус круга одинаковы. Поэтому радиус круга равен одной из сторон шестиугольника. Обозначим его как а.
Тогда площадь круга будет равна: S = 3,14 * а^2.

б) Для нахождения площади сектора круга, нам необходимо знать центральный угол сектора. Если мы внимательно посмотрим на рисунок, мы увидим, что центральный угол сектора равен 120°. Для расчета площади сектора, мы используем формулу: S=πr^2 * (α/360), где S - площадь сектора, π - математическая константа, равная примерно 3,14, r - радиус круга, α - центральный угол сектора.
Так как шестиугольник является правильным, все его стороны и радиус круга одинаковы. Поэтому радиус круга равен одной из сторон шестиугольника. Обозначим его как а.
Тогда площадь сектора будет равна: S = 3,14 * а^2 * (120/360).

в) Для нахождения площади части, расположенной вне круга, мы должны сначала найти площадь всего шестиугольника, а затем вычесть из нее площадь круга. Если мы внимательно посмотрим на рисунок, мы увидим, что шестиугольник является правильным и стороной шестиугольника является радиус круга. Обозначим его как а.
Площадь шестиугольника равна: S = (3√3/2) * а^2.
Тогда площадь части, расположенной вне круга, будет равна: S = (3√3/2) * а^2 - 3,14 * а^2.

Таким образом, чтобы решить задачу, нам необходимо знать значение стороны шестиугольника. Если указано в условии задачи, можно использовать это значение для расчетов. Если же не указано, то нам необходимо знать дополнительную информацию для нахождения значения а.