№8. Докажите, что производная четной функции нечетна, а производная нечетной функции, напротив, четна.
Б) Верны ли обратные утверждения:
1) если f’ (x) – четная функция, то f (x) – нечетная функция;
2) если f’ (x) – нечетная функция, то f (x) –четная функция?
Задание №9
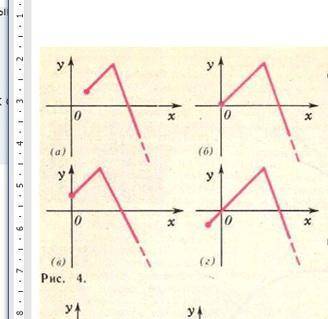
Достройте график функции, изображенный на рисунке 4, до графика всюду определенной, непрерывной на R и
1) четной функции;
2) нечетной функции.
В каких случаях это невозможно? В каких случаях это можно сделать несколькими Известно, что функция f всюду определена, четна и периодична с периодом Т=4. Восстановите ее график по участку, изображенному на рисунке 5. В каких случаях это нельзя сделать? В каких случаях это можно сделать, но неоднозначно?
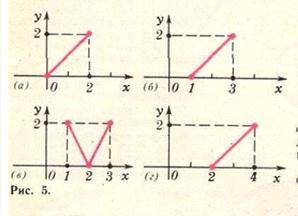
Ответы
Показать ответы (3)
Другие вопросы по теме Алгебра
Популярные вопросы
- А) в равнобедренном треугольнике периметр равен 36 см, а основание 10 см....
1 - Световое табло состоит из лампочек каждая из которых может находиться в трех...
3 - Нужно разобрать как часть речи слова небо,земля,леса....
2 - Закончите разложение данного числа на простые множители(используйте степени)...
1 - Просклоняйте имена существительные в единственном числе зима,осень, лето?...
1 - Как написать ро где ты катаешься на коньках?...
3 - Решить для ремонта квартиры купили 8 рулонов обоев длиной по 10 м 50 см....
2 - Где нужно поставить запятые. и не только потому что у нас есть общие увлечения...
3 - Правило деления десятичных дробей на смешаное число...
1 - Составте уровнение дисоциации следующих веществ rboh...
2