50 решите неравенства 1.^{-1}) 2.
2.
Другие вопросы по теме Алгебра
Популярные вопросы
- 2предложения со словом трудолюбивый и ленивый....
1 - Проспрягайте слова две тетради , три гектара , четыре яблока по падежам !...
1 - Уменя вопрос по , какие буквы являются шипящими и когда можно сокращать полную...
2 - 1) 1,1x-2целых1/2=3/5x 2) 6,75x=2целых 1/4x-9 (решить уравнение) 20 с меня...
2 - Какие факторы влияли на этот процесс? как формировалось сословие общество...
2 - целых плюс восемь седьмых!...
3 - Сочинение по картине в.п. фельдмана «родина»...
3 - К150 г 10%-ного раствора соли прибавили 25г соли. вычислите массовую долю...
3 - Эссе какую роль сыграл пётр 1 в развитии наук и образовании?...
3 - Кто умней лисица или ворона (отвечать по буквам )( в-ворона,л-лисица)...
3
ответ:![x \in [1; \ 5]](/tpl/images/0205/7464/e62de.png)
ОДЗ: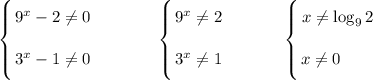
Замена: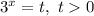
ОДЗ: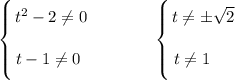
По методу интервалов выясняем знаки неравенства и получаем:
Обратная замена:
Объединяем все три условия и получаем:
ответ:![x \in \bigg[\log_{3}\dfrac{1}{2}; \ 0 \bigg) \cup (\log_{3}\sqrt{2}; \ 1]](/tpl/images/0205/7464/ef558.png)