1. Алгебра
  2. [50 б]. нужно сделать

[50 б]. нужно сделать по образцу ​

nankasvanka nankasvanka    2   16.11.2019 00:20    0

Ответы
пожирательзнаний1 пожирательзнаний1  10.10.2020 13:44

ответ: во вложении Объяснение:


[50 б]. нужно сделать по образцу ​
ПОКАЗАТЬ ОТВЕТЫ
ivanchistyakov ivanchistyakov  10.10.2020 13:44

\displaystyle 1) \ y^5-8x^4=0 \Rightarrow 5y^4y'-32x^3=0 \Rightarrow \boxed{y'=\frac{32x^3}{5y^4}}

\displaystyle 2) \ x^8+y^{13}-2=0 \Rightarrow 8x^7+13y^{12}y'=0 \Rightarrow \boxed{y'=-\frac{8x^7}{13y^{12}}}

\displaystyle 3) x^{12}siny+y^{10}=0 \Rightarrow 12\cdot x^{11}\cdot siny+x^{12}\cdot cosy\cdot y' + 10\cdot y^9\cdot y'=0 \Rightarrow \\ \Rightarrow 12\cdot x^{11} \cdot siny +y'(x^{12}\cdot cosy + 10\cdot y^9)=0 \Rightarrow \boxed{y'=-\frac{12\cdot x^{11}\cdot siny}{x^{12}\cdot cosy+10\cdot y^9}}

\displaystyle 4)y^7+x^5cosy=0 \Rightarrow 7y^6y'+5x^4cosy-x^5siny\cdot y'=0 \Rightarrow \\ \Rightarrow y'(7y^6-x^5siny)=-5x^4cosy \Rightarrow \boxed{y'=-\frac{5x^4cosy}{7y^6-x^5siny}}

\displaystyle 5) x^9y+xy^{12}=9 \Rightarrow 9x^8y+x^9y'+y^{12}+12xy^{11}y'=0 \Rightarrow \\ \Rightarrow 9x^8y+y^{12}=-y'(x^9+12xy^{11}) \Rightarrow \boxed{y'=-\frac{9x^8y+y^{12}}{x^9+12xy^{11}}}

То есть главное - брать производную в обычном порядке.  Вспомним вот эту формулу: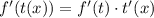 f'(t(x))=f'(t)\cdot t'(x), она тут очень даже

Вот, например, когда берется производная

(f(y))'=f'_y\cdot y', что делалось во всех заданиях.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
vlad369cool vlad369cool  04.03.2022 12:47
Дана функция у=х²-2х-8 Не строя графика, найдите: a) область определения функции. b) нули функции. с) наименьшее значение функции....
NadiaU0 NadiaU0  11.06.2019 06:50
100 ! трое друзей покупали музыкальные инструменты. первый внёс а рублей, второй на 10% больше, чем первый, а третий - на 40% меньше, чем оба его друга внесли вместе....
Samatova03 Samatova03  11.06.2019 06:50
Решить неравенство (x+2)^2*(x+4) меньше или равно 0...
uhanovauliana05 uhanovauliana05  11.06.2019 06:50
При яких значеннях х виконується рівність: │х + 5│= х + 5 ? а) при будь-якому х, не більшому за –5; б) при будь-якому х; в) при будь-якому х, не меншому за –5; г) при...
Levix322 Levix322  11.06.2019 06:50
Найдите значение выражения 16а+1у при а =1/8,y=-1/6...
q1412201428 q1412201428  11.06.2019 06:50
Графики функций y=kx+3 и y=5-3x параллельны. а) найдите коэффициент k. б) постройте оба графика на одной координатной плоскости...
kurmangazievbeka kurmangazievbeka  11.06.2019 06:50
Отрезок, длина которого равна а, разделён на три неравных отрезка. найдите расстояние между серединами этих отрезков....
никуся1984 никуся1984  25.07.2019 00:40
Разложите многочлен на множители: (решение+ответ) 1) a³+a²-a-1 2) a³+b³-a²b-ab²...
ян6 ян6  25.07.2019 00:40
5,3×8,2^2-5,3×1.8^2: 10.6×6.6^2-10.6×3.4^2...
adelya63Ada adelya63Ada  25.07.2019 00:40
Решить 1)исследовать функцию на молотонность и экстремумы у=2х*inx 2)найти угловой коэффициент касательной к графику функции у= х^3+27 в точке пересечения этого графика...

Популярные вопросы