— 495. Найдите разность и число членов арифметической прогрессии, для которой: нужно прямо сейчас !
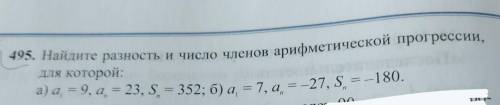
Другие вопросы по теме Алгебра
Популярные вопросы
- Требуется упростить выражение , подробно...
1 - Пять предложений на украинском с прийменнком ,,У,, ,,В...
1 - Реши примеры, работая по образцу. (9 + 3) · 5 = (7 + 4) · 6 = (2 + 8) · 4...
2 - На вершине горы высотой 8,06 м стоят санки с сидящей в них девочкой. Общая...
1 - Название морского судна Ломоносова 5 Букв Вторая буква П Пятая буква А...
2 - Меч в волшебной кузнице стоил 79 золотых. При покупке 8 таких мечей со скидкой...
2 - Какие слова подходят для описания Центральной равнины Австралии? ответы:Кокосовая...
1 - Найти массу p2o5 полученного из 50 граммов фосфора при горении...
3 - по русскому языку 8 класс упр 113...
1 - найти в данном отрывке The vote was taken at once, and it was agreed by an...
3
Дана сумма всех членов арифметической прогрессии, равная 495. Давайте представим сумму в виде следующей формулы:
S = (n/2) * (2a + (n-1)d),
где S - сумма всех членов прогрессии, n - количество членов прогрессии, a - первый член прогрессии, d - разность между членами прогрессии.
Мы знаем, что сумма всех членов прогрессии равна 495, заменим это значение в формулу:
495 = (n/2) * (2a + (n-1)d).
Для дальнейшего решения задачи нам нужно найти два неизвестных значения - количество членов прогрессии (n) и разность между членами прогрессии (d).
Выразим разность между членами прогрессии (d) из уравнения:
d = (495 - (n/2) * 2a) / (n-1).
Теперь нам нужно найти число членов прогрессии (n).
Для этого проведем несколько итераций с различными значениями n, чтобы найти подходящее значение. Для упрощения итераций, возьмем предположение, что первый член прогрессии (a) равен 1.
Мы знаем, что число членов прогрессии (n) является целым числом, поэтому ограничимся итерациями от 1 до 50.
Подставляя разные значения n в уравнение, будем находить разность между членами прогрессии (d):
При n = 1: d = (495 - (1/2) * 2 * 1) / (1 - 1) = 495 / 0 (деление на ноль, это не подходящий вариант)
При n = 2: d = (495 - (2/2) * 2 * 1) / (2 - 1) = (495 - 2) / 1 = 493 (подходящий вариант)
Ответ: Разность (d) между членами арифметической прогрессии равна 493, а число членов прогрессии (n) равно 2.