40 отрезки ab и cd являются окружности. найти cd ,если ab =12, а расстояние от центра окружности до хорд ab и cd равны соответственно 8 и 6
Другие вопросы по теме Алгебра
Популярные вопросы
- Определите массу кислоты которую можно получить путём полного бромирования...
3 - Дан отрезок AL. Назови симметричные точки относительно точки H....
3 - Modal Verbs. 14 .Circle the correct item....
2 - Напишите рассказ о хорошей речи 10-16 предложений...
3 - III. Fill in with :1) am/is/are1. There__ some cans of tuna fish...
2 - Верно ли утверждение? Если одна из двух параллельных прямых параллельна...
1 - 8. (0,5 points for the correct task) Read the text. Choose from...
1 - Накреслить 3 видризка .Довжина видрізка АВ становить 9 см., відрізок...
2 - Предмет: финансы организаций...
2 - Уравнение синтеза аминокапроновой килоты из пропана...
1
Пусть О — центр окружности, OM = 8 и ON = 6 — перпендикуляры к хордам AB и CD соответственно. Треугольники AOB и COD равнобедренные, значит, AM = MB иCN = ND.
Тогда в прямоугольном треугольнике MOB имеем
В прямоугольном треугольнике CON гипотенуза CO = OB = 10, откуда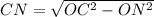 Получаем, что CD = 2CN = 16 .
Получаем, что CD = 2CN = 16 .
ответ: 16