1. Алгебра
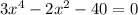  2. 3x⁴-2x²-40=0 розв язати рівняння

3x⁴-2x²-40=0 розв'язати рівняння

назар173 назар173    3   12.09.2021 15:36    0

Ответы
mashamelnik28 mashamelnik28  12.09.2021 15:40

Пусть t=x^2, тогда 3x^4-2x^2-40=0 будет

3t^2-2t-40=0

Находим дискриминант:

D=4+4*3*40

D=484=22^2

Используем формулу для корней кваратного уравнения:

t=\frac{2+-22}{6}

t_{1}=4

t_{2}=-\frac{10}{3}

Мы помним, что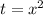 t=x^{2} ⇒

x^{2}=4

x_{1} =4\\x_{2} =-4

Это все вещественные решения данного биквадратного уравнения, но если нужны ещё и комплексные, то к предыдущим двум решения добавляются ещё два:

x^{2}=-\frac{10}{3}\\x_{1} =\sqrt{\frac{10}{3}}i \\x_{2} =\sqrt{-\frac{10}{3}}i

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
nazarpetrenko1 nazarpetrenko1  21.07.2019 00:50
Докажите неравенство тема квадратные неравенства 1) (6y-1)(y+2) (3y+4)(2y+1) 2)(3x-1)(2x+1) (2x-1)(2+3x)...
марго170 марго170  21.07.2019 00:50
Вычислите sin 202 градусов 30 минут...
cooldasha11042 cooldasha11042  21.07.2019 00:50
Решите уравнение а) (5x-2)(5x+-1) в квадрате=4 б) 100х в квадрате -16=0...
ВоительЧерноснежка ВоительЧерноснежка  21.07.2019 00:50
Решите методом сложения - x -9y=33 9y-x=-21...
bosyakostya bosyakostya  21.07.2019 00:50
Замените звездочку в выражении 64+32x+* таким одночленом чтобы полученное выражение можно было представить в виде квадрата двучлена....
Лагуна2222 Лагуна2222  21.07.2019 00:50
Сеще одним уравнением не пойму, как решить, объясните...
2ArtemPetrenko2 2ArtemPetrenko2  21.07.2019 00:50
Решить уравнение, , 1/5x + 18 = 1/55x - 29 заранее...
Deeplace Deeplace  21.07.2019 00:50
Найдите координаты точек пересечения графиков функции у=-х^2+2х-3 с осью орди...
BakerTaka BakerTaka  14.06.2019 18:10
Как с такого случая ax-ay-bx+by, перейти к такому (a-b)(x-y)?...
evelina2112 evelina2112  14.06.2019 18:10
2х-у = при х= 0.4,у=-5 ху ниже числа 2х-у идёт дробная черта! нужно найти значение выражения...

Популярные вопросы