3.Упростите выражение: (cos2a - ctg2a)•sin2a. 2.Найдите значение: 3 tg - - sin2 600 + cos co25- ctg230°
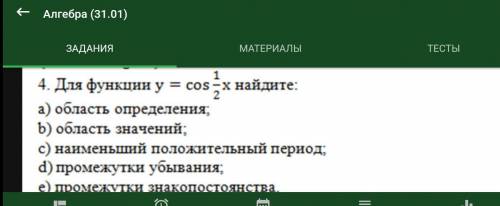
. Для 4. Для функции у = cos - х найдите: a) область определения, b) область значений; c) наименьший положительный период .
Другие вопросы по теме Алгебра
Популярные вопросы
- 1.Мәтінді мұқият оқып төмендегі берілген тапсырмаларды орындаңыз ЭТО...
1 - Жаратылыстану комектесип жиберинниздерши...
1 - История Казахстана Сор :)...
3 - 44cupadails pleapin a • Даналык - Іerl акылга салып, тиянактыereir...
3 - Теңдеуді шешіңіз 12×|2x-5|=-60...
2 - Описание рок оперы Юнона и Авось...
2 - Почему чуму изображали как человека с головой ворона?Просто интересно...
1 - Адамның іс әрекетінің не реттейд...
1 - В ряд стоят 7 коробок, в которых по порядку лежат 1,2,3,4,5,6 и 7...
2 - Diamond Os Определите химические связи в соединении на основе типа...
2
1. Упростите выражение: (cos2a - ctg2a)•sin2a.
Для начала воспользуемся известными тригонометрическими формулами:
- cos(2a) = cos^2(a) - sin^2(a)
- ctg(2a) = (cos(2a))/(sin(2a))
- sin(2a) = 2sin(a)cos(a)
Подставим их в наше выражение:
(cos(2a) - ctg(2a))•sin(2a) = (cos^2(a) - sin^2(a) - (cos(2a))/(sin(2a)))•(2sin(a)cos(a))
Для удобства расчетов сократим дробь на sin(2a):
(cos^2(a) - sin^2(a) - 2cos^2(a))/(sin(a))•(2cos(a))
Далее сгруппируем подобные слагаемые:
(-sin^2(a) - cos^2(a))/(sin(a))•(2cos(a))
Теперь мы можем использовать две тригонометрические формулы:
- sin^2(a) + cos^2(a) = 1
- sin(a)cos(a) = 1/2sin(2a)
Подставим их и упростим наше выражение:
(-1)/(sin(a))•(2cos(a)) = -2cos(a)/(sin(a))
Итак, упрощенное выражение равно -2cos(a)/(sin(a)).
2. Найдите значение: 3 tg - - sin^2(600) + cos(co25) - ctg(230°).
Для начала разберемся с функцией tg(-):
tg(-θ) = -tg(θ)
Подставим это в наше выражение:
3(-tg(600)) + sin^2(600) + cos(co25) - ctg(230°)
Заметим, что sin^2(600) = sin^2(600-360) = sin^2(240) = sin^2(240-180) = sin^2(60). Также, tg(600) = tg(240).
Подставим и это и продолжим расчеты:
-3tg(240) + sin^2(60) + cos(co25) - ctg(230°)
Мы знаем, что tg(240) = - tg(60), а ctg(230°) = -ctg(-50°).
Продолжим расчеты:
-3(-tg(60)) + sin^2(60) + cos(co25) - (-ctg(50))
3tg(60) + sin^2(60) + cos(co25) + ctg(50)
Теперь используем известные значения:
tg(60) = sqrt(3)
sin^2(60) = 3/4
cos(25) ≈ 0.9063
ctg(50) = 1/tg(50) = 1/(1.1918) ≈ 0.8391
Подставим и рассчитаем:
3sqrt(3) + 3/4 + 0.9063 + 0.8391 ≈ 3.3668
Таким образом, исходное выражение равно примерно 3.3668.
3. Для функции у = cos(-х) найдите:
a) область определения,
b) область значений,
c) наименьший положительный период.
a) Область определения:
Функция у = cos(-х) определена для всех действительных чисел, так как аргумент функции может быть любым числом.
b) Область значений:
Значения функции cos(x) находятся в пределах от -1 до 1. Так как функция у = cos(-х) является симметричной относительно оси ординат, область значений остается такой же, от -1 до 1.
c) Наименьший положительный период:
Наименьший положительный период функции cos(x) равен 2π. Так как функция у = cos(-х) является симметричной относительно оси ординат, наименьший положительный период также равен 2π.
Надеюсь, что мой ответ был понятен и полезен! Если у вас возникнут еще вопросы, не стесняйтесь задавать их.