3.41. Найдите область определения функции:
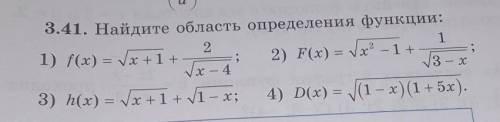
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько г C2H5OH получится при гидратации 500мл C2H4?...
2 - Хлорбензен+1 хлорбутан+натрій=...
3 - Как назвали женщину которая управляла страной...
3 - Inscape редакторында қандай құрал саймандар бар? ...
1 - Какова масса куска льда объёмом 0,4 метра в кубе,если плотность льда...
2 - He ___ looking at her, wondering where he ___ her * kept / had seenkeeps...
1 - A) 63: (-21); B) -0,32.5: 1.3:б)-24: (-6);г) - 7 6/7:(-9 3/7)...
3 - Заполните таблицу, приведите примеры предприятий, функционирующих в...
1 - Тірек сөздерді қолданып, сөйлемдерді толықтыр. Тірек сөздер: балқу,...
2 - 4. Когда сосуд массой 600 г целиком наполнили бен- зином, его масса...
2
В данном случае у нас есть функция f(x), заданная формулой:
f(x) = √(9 - 4x^2)
Для того чтобы вычислить область определения этой функции, нужно учесть два фактора:
1. Ограничение по определению корня: извлечение корня имеет смысл только для неотрицательных чисел или нуля. Значит, выражение (9 - 4x^2) должно быть больше или равно нулю.
9 - 4x^2 ≥ 0
2. Ограничение по определению аргумента: знаменатель не должен равняться нулю, так как деление на ноль не определено. Значит, рассмотрим условие:
9 - 4x^2 > 0
Перейдем к решению первого неравенства:
9 - 4x^2 ≥ 0
Для упрощения неравенства, перенесем все в левую часть:
4x^2 - 9 ≥ 0
Выражение в левой части разности можно преобразовать к виду разности квадратов:
(2x - 3)(2x + 3) ≥ 0
Рассмотрим значения, при которых произведение двух множителей положительно или равно нулю.
1) Если (2x - 3) ≥ 0 и (2x + 3) ≥ 0, то оба множителя отрицательны или равны нулю:
2x - 3 ≥ 0 => 2x ≥ 3 => x ≥ 3/2
2x + 3 ≥ 0 => 2x ≥ -3 => x ≥ -3/2
2) Если (2x - 3) ≤ 0 и (2x + 3) ≤ 0, то оба множителя положительны или равны нулю:
2x - 3 ≤ 0 => 2x ≤ 3 => x ≤ 3/2
2x + 3 ≤ 0 => 2x ≤ -3 => x ≤ -3/2
Итак, область определения функции f(x) состоит из значений x, для которых выполняются все полученные неравенства одновременно.
Вариант 1: x ≥ 3/2 и x ≥ -3/2
То есть, область определения включает все значения x, которые больше или равны 3/2.
Вариант 2: x ≤ 3/2 и x ≤ -3/2
То есть, область определения включает все значения x, которые меньше или равны -3/2.
2) Учитывая ограничение по определению аргумента, рассмотрим второе неравенство:
9 - 4x^2 > 0
Для упрощения неравенства, перенесем все в левую часть:
4x^2 - 9 < 0
Как и в предыдущем случае, выражение в левой части можно преобразовать к виду разности квадратов:
(2x - 3)(2x + 3) < 0
Рассмотрим значения, при которых произведение двух множителей отрицательно.
1) Если (2x - 3) > 0 и (2x + 3) < 0, то один множитель положителен, а второй отрицателен:
2x - 3 > 0 => 2x > 3 => x > 3/2
2x + 3 < 0 => 2x < -3 => x < -3/2
2) Если (2x - 3) < 0 и (2x + 3) > 0, то один множитель отрицателен, а второй положителен:
2x - 3 < 0 => 2x < 3 => x < 3/2
2x + 3 > 0 => 2x > -3 => x > -3/2
Таким образом, область определения функции f(x) состоит из значений x, для которых выполняется второе неравенство.
Вариант 1: x > 3/2 и x < -3/2
То есть, область определения включает все значения x, которые больше 3/2 и меньше -3/2.
Вариант 2: x < 3/2 и x > -3/2
То есть, область определения включает все значения x, которые меньше 3/2 и больше -3/2.
Итак, область определения функции f(x) складывается из пересечения областей, полученных в каждом случае.
Область определения функции f(x) состоит из всех значений x, которые больше или равны 3/2, и меньше или равны -3/2.
Окончательно, область определения функции f(x): x ≥ 3/2 и x ≤ -3/2.