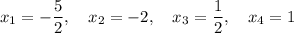(2x^2+3x)^2-7(2x^2+3x)= -10 решите и обьясните
Другие вопросы по теме Алгебра
Популярные вопросы
- напишите письмо мальчикам в котором бы вы обсудили с ними волнующие...
2 - ЕлЬНЫМИ. 3. Что на что похоже? Допишите предложения, используя...
3 - Пример:прыгнуть высоко — наречие, обстоятельство;дерево высоко...
1 - Шұғаның белгісі кейіпкерлеріне мінездемеШұға, Əбдірахман, Айнабай,...
3 - Разложите на множители методом группировки 3а+6+ав+2в...
1 - Продолжите предложения: Коллектив нужен … Коллективы возникают...
2 - В коло вписано трикутник ABC, у якому проведено медіани AF і ВК.Медіану...
3 - тұғжан қандай кейіпкер?өзіміз оқыған шығармаларда тұржан сияқты...
1 - Известно, что две параллельные прямые пересекаются третьей прямой,...
1 - решить (не советуйте приложение...
3
Сделаем замену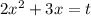 :
:
Решим это уравнение через дискриминант:
Вернёмся к исходной переменной. Сначала разберём случай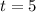 :
:
Теперь разберём случай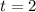 :
:
ответ: