298. Решите показательное неравенство с дополнительной переменной
b)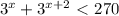
h)![4*4^{x]-2\geq 7*2^{x}](/tpl/images/3963/5855/0ba7b.png)
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Anyway, I’ve got some great news! My team won the local football...
2 - 1. 60гр SO22. 0.25 моль NO2...
3 - Task 2. Choose the correct form of the verb Lion: Did Anna 1)...
2 - Берілген сөйлемдерді жалғастырып, мәтіндегі оқиғаны 5-6 сөйлеммен...
1 - C) к крючку С, к которому привязан конец веревки?...
3 - Мәтінің баяндау желісін сақтап әр бөлігінен тезис жаз...
2 - 30 - х = 15 Знайти невідоме...
1 - Задание No 2 Укажите утверждения, которые соответствуют текстуДурыс...
3 - Объем каждого куба равен 1 см в кубе. Чему равен объён данных...
2 - Что говорится в 7 главе Конституционного Закона «О государственной...
2
Объяснение:
b)
ответ: x∈(-∞;3).
h)
Пусть 2ˣ=t ⇒
ответ: x∈[1;+∞).