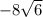24*(sin 15 - cos 15)/cos 30 =
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите корень уравнения ...
3 - Диаметр колеса велосипеда равен 50 см. велосипедист проехал 314м. тогда...
1 - решить кросворд по информатике QwQ...
3 - Вычислить длину дуги параболы y=-x^2+4 A(1;3) B(2;0)...
1 - 186 Listen and match. There is one extra job.Children Jobs they would...
1 - Який шлях проходить світловий промінь у воді з показником 4/3 за 0,1...
1 - Задание 2. Как написать рассказ Опираясь на материалы видеоконсультации,...
2 - Про що свідчить довжина варіаційного ряду?...
3 - Label the pictures.river rock mausoleum building kingdom...
2 - Смысл пословицы Не рискнешь дела Не совершить струсишь через арык не...
2
Объяснение:
24*(sin 15 - cos 15)/cos 30 = 24*( sin(60°-45°) - cos(60°-45°) ) /cos 30° =
Используем формулу: sin (x-y) = sin x * cos y - cos x * sin y
cos (x-y) = cos x * cos y + sin x * sin y
= 24* ( (sin 60 *cos 45 - cos 60 * sin 45) - (cos 60 * cos 45 + sin 60 * sin 45) ) /cos 30 = 24* (sin 60 *cos 45 - cos 60 * sin 45 - cos 60 * cos 45 - sin 60 * sin 45 ) /cos 30 = 24*( ) /
) / 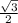 = 24*( -
= 24*( -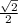 ) /
) / 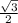 =
= 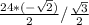 =
= 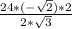 =
= 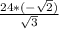 =
= 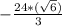 =
=