23. В геометрической прогрессии со знаменателем q = 2 сумма первых пяти членов равна 155. Найдите шестой член этой прогрессии. ВАРИАНТ ОТВЕТА
А 240
B 560
С 160
D 320
E 80
Другие вопросы по теме Алгебра
Популярные вопросы
- Объясни значение выражения закончить работу в срок...
1 - Решить корельская береза занимает 69/85 сотых всех площадей...
3 - Рассказ на казахском языке про часы...
3 - 6. в каком предложении есть неоднородные определения ( знаки...
3 - Составить хронологическую таблицу народных вступлений при петре...
1 - Какое число может поделиться на 2 и 3 и 7...
2 - Укажите морфологические признаки слова !...
1 - Что пройдёт с чистой холодной водой,налитой в сосуд,который...
3 - Водной системе координат постройте графики уравнений 3x-2y+6=0,...
2 - На сколько минут 3ч больше 3 мин? на сколько секунд 5 мин больше...
3
Формула n-го члена геометр. прогрессии: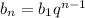 ,
, 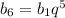 .
.
Cумма n членов геом. прогрессии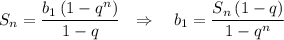 .
.
s=b₁*(qⁿ-1)/(q-1)
s₅=b₁*(q⁵-1)/(q-1)
155=b₁(32-1)/1⇒b₁=155/31=5
bn=b₁*qⁿ⁻¹
b₆=b₁*q⁵
b₆=5*2⁵=5*32=160 -ответ C