100 ! ! решите два номера #7.15 и 7.16
Другие вопросы по теме Алгебра
Популярные вопросы
- Для приготовления 4 кг варенья из вишни требуется 2400г сахарного...
2 - Каким образом партии большевиков удалось удержать власть после...
2 - Сделайте с условием пол длиной 12 м и шириной 8м надо покрыть квадратными...
1 - X: 6-246=132 мне через 10 мин в школу 54: m+734=740 873-n: 9=549...
2 - Товар стоил 1500 рублей . после снижения цены он стал стоить 1200...
3 - Из одного пункта одновременно в одном направлении выехали два автомобиля.скорость...
2 - Фанатический разбор слова: ракета разбирать так: гласная(согласная),звонкая(глухая),парная(не...
1 - 3т4ц-245кг + 10ц 28кг 11км 4 м -356 м +9км 56м= 8 ч 15мин -2час...
2 - 1д- 45% 2д-30% остатка осталось-? всего- ? ответы: а)38% б)13,5%...
2 - Запишите десятичную дробь в виде процентов 0,7 0,65 0,02 запишите...
1
7.15
ответ: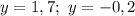
ответ: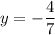
ответ: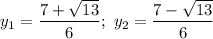
ответ: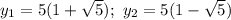
7.16
ответ: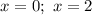
(Можно также решить, раскрывая скобки в каждом выражении. Также можно решить, приписав квадратный корень к обеим частям уравнения, тогда получиться в обеих частях модуль, согласно правилу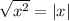 )
)
ответ: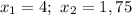
ответ: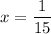
ответ: