1.Прямая L задана уравнением (x−3)/4=(y−4)/6=(z−1)/4 плоскость «α» уравнением: 2x+3y+2z−1=0 Каково взаимное расположение прямой и плоскости? 2.Плоскость «α» задана уравнением: 3x+2y−4z+2=0 тогда скалярное произведение ее нормального вектора на вектор b=(2; 1; 0) равно
Другие вопросы по теме Алгебра
Популярные вопросы
- Квадрат обертається навколо сторони. Знайдіть площу поверхні та...
1 - График обратной пропорциональности походит через точку с координатами(3;5).Найдите...
3 - Подберите к этим словам антонимы на казахском...
3 - склад мінералу описує формула Mg4(So4)4f2. виходячи з принципу...
3 - Краткое содержание фильма Алёша...
3 - Образ Кліві з твору запах думки очень надо побыстрее!...
3 - Винесіть множник під знак кореня ...
2 - В) летние каникулы, отдых и веселье, маг C) летние каникулы, в...
2 - 4. Что происходит в хижине ночью A) в окна хижины лезет разная...
1 - Известны координаты трех вершин ромба КМРС: К(1;5), М(2;5), Р(3;1)....
1
1. Прямая и плоскость перпендикулярны.
2.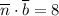
Объяснение:
Прямая
имеет направляющий вектор
Плоскость
2x + 3y + 2z - 1 = 0
имеет нормаль
Условие перпендикулярности прямой и плоскости:
выполняется
Следовательно, прямая и плоскость перпендикулярны
2.
Плоскость
3x + 2y - 4z + 2 = 0
имеет нормаль
Скалярное произведение