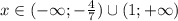1.Найдите площадь треугольника,у которого стороны 13см и 6см,а угол между ними 30° 2.Решите неравенство 7х^2-3х-4>0
Другие вопросы по теме Алгебра
Популярные вопросы
- Вставьте пропущенные слова...
3 - Розкласти на обиколиники b) (x - 2) + x ² – 140 + 49. – Ebappam pizoeageа)...
3 - 1) Вычисли y(4), если y(p)= −8,7−p. y(4)= 2) Раскрой скобки −(a−b)−(c+d)+(−e+f):...
3 - Киіз үй – көшпелілердің баспанасы Киіз үйдің пайда болуы қола дәуірінен басталады...
1 - Найдите пары равных треугольников и докажите их равенство...
3 - Упростите выражение: 1) 1+sin²a+cos²a; 2) sin²a / 1-cos²a ; 3) 1-sin²a/cos²a...
2 - Казак тили 7 сынып 73 бет 6 тапсырма...
3 - Які географічні назви згадано Іван Підкова ...
1 - Серед наведених речень укажіть просте: А) Промайнуло літо і осінь, сходить...
1 - Два текста содержат одинаковое количество символов. Первый текст составлен...
2
Объяснение:
1) Воспользуемся формулой площади треугольника:
Имеем а=13 см; b=6 см; α=30°
2) Дано неравенство:
7х²-3х-4>0
Найдем корни:
Отметим на числовой оси полученные корни. Неравенство строгое, поэтому сами корни в ответ не входят.
Найдем знаки выражения на промежутках:
⇒