1 и 3, распишите как делать
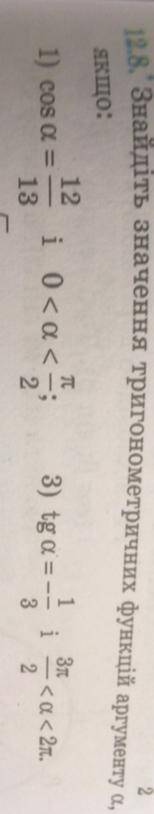
Другие вопросы по теме Алгебра
Популярные вопросы
- Представьте, что вы хотите поделиться своим мнением о дружбе...
1 - Проверь, как ты научился находить орфограммы в тексте и писать...
3 - вобраз витаута у творы пахлава витаута . 25 ....
2 - Аб в гукажіть рядок, у якому дієприкметник утвореноправильно.а...
2 - Как меняется настроение героя зимнего вечера от начала к концу...
1 - Замените словосочетание построенное на основе согласования синонимичным...
3 - Евгений базаров причина появления в обществе и образа нового...
2 - Geri everyone in this street. a. knows b. met c. know d. meet...
1 - Выпісаць па тры словазлучэнні розных відаў і разабраць...
2 - На стороне ef параллелограмма defg взята точка m так,что de=em....
1
1.
угол принадлежит 1 четверти, значит все тригонометрические функции положительны.
3.
угол принадлежит 4 четверти, значит косинус положительный, синус и котангенс отрицательные.
формула: