1) √72•√2
2) √360•√490
3) √40/√0,025
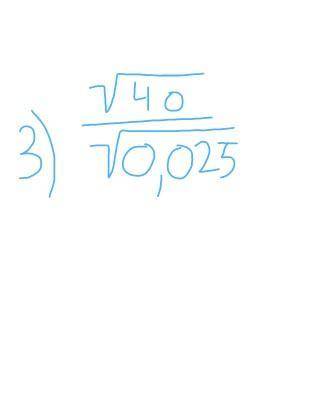
Другие вопросы по теме Алгебра
Популярные вопросы
- Якби Маруся Чурай сказала про себе що вона щаслива людина чи погодились...
3 - Приготувати 80 г розчину кухонної солі з масовою часткою 0,2 очень...
2 - Если не сложно Контрольна робота. Творчість Тараса Шевченка Початковий...
3 - Чи відповідає Указ Президента #140/2021 про введення в дію рішення...
3 - Организация М создана на основе объединения капиталов учредителей,...
3 - Чи вважаєте ви що наказ номер 227 був правильним і своєчасним кроком...
2 - В таблице приведены запросы и количество страниц, которое нашёл...
3 - Накресліть кут A, градусна міра якого дорівнює 40°, і побудуйте...
3 - Условие к задаче Между Москвой и Петербурга расположен город Тверь...
2 - Трактор має вагу 58кH.Який тиск він чинить на грунт якщоплоща його...
1
1) √72•√2
Для начала, мы можем упростить корень из 72. Разложим 72 на простые множители: 72 = 2^3 * 3^2. Теперь мы можем вынести корень из каждого множителя отдельно: √2^3 * √3^2.
Однако, для того чтобы применить правило упрощения, важно помнить, что корень из произведения двух чисел равен произведению корней отдельных чисел. Таким образом, наш выражение становится: √2^3 * √3^2 = 2√2 * 3 = 6√2.
Теперь у нас есть новое выражение: 6√2•√2. Мы знаем, что корень квадратный из числа равен самому числу. Так что √2 * √2 = 2.
Итак, наше окончательное решение будет: 6 * 2 = 12.
Ответ: 12.
2) √360•√490
Аналогично, мы начнем с упрощения корней каждого числа по отдельности. Давайте разложим 360 и 490 на простые множители.
360 = 2^3 * 3^2 * 5
490 = 2 * 5 * 7^2
Теперь мы можем вынести корни отдельно: √2^3 * √3^2 * √5 * √5 * √7^2.
Упрощая корни, получаем: 8√5 * 5 * 7.
Продолжим упрощение: 8 * 5 * 7 = 280.
Ответ: 280.
3) √40 / √0,025
Для начала, возьмем корни отдельно:
√40 = √4 * √10 = 2√10
√0,025 = √0,05 * √0,05 = 0,1 * 0,1 = 0,01
Теперь делим один корень на другой: (2√10) / 0,01
Чтобы разделить один корень на другой, мы можем умножить числитель и знаменатель на обратное значение второго корня. Таким образом, получаем: (2√10 * 10) / (0,01 * 10) = (20√10) / 0,1
Упрощаем выражение: 20 * √10 / 0,1 = 200√10.
Ответ: 200√10.
Верю, что эти объяснения помогут вам лучше понять решение задач. Если у вас возникнут еще какие-либо вопросы, не стесняйтесь задавать.