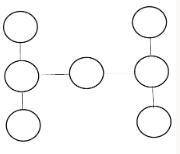
Паша и Даша ищут 7 чисел (которые не повторяются) от 1 до 9, так что на следующем рисунке получается, что произведение трех чисел в каждом столбце равно произведению трех чисел в центральной строке.
Другие вопросы по теме Математика
Популярные вопросы
- Мини сочинение на тему двухпартийная политическая система виги и тори. (насколько...
2 - Реферат по музыке на тему искусство память человечества...
3 - Составь предложения из данных слов. начинай предложение по-разному. приходит,...
1 - Вычислите массовую долю кислорода в соединении nho2...
2 - Сочинение объявление о грузоперевозках...
1 - Сумма двух углов образовавшихся при пересечении двух прямых равна 122°найдите...
3 - На одной полке -5 книг а на другой -4 раза больше сколько книг на двух полках...
1 - Знайдіть в переліку зайве слово. а. 1) глюкоза; 2) рибоза; 3) дезоксирибоза;...
3 - Комната имеет форму квадрата вдоль стен нужно расставить 10 стульев так чтобы...
3 - Выпеши из толокового словаря значения многозначного слова багаж...
2
Числа от 1 до 9:
1, 2, 3, 4, 5, 6, 7, 8, 9
Дело в том, что среди этих чисел есть простые множители: 1, 2, 3
И есть числа, которые можно разложить на простые множители 1, 2, 3:
4 = 2•2
6 = 2•3
8 = 2•2•2
9 = 3•3
НОК (4;6;8;9) = 3•3•2•2•2 = 72
А всего чисел как раз 7:
1, 2, 3, 4, 6, 8, 9
Можно написать, что
1•8•9 = 72
2•4•9 = 72
3•4•6 = 72
А теперь распределим эти числа в два столбца и одну строку.
Поскольку 9 и 4 встречаются по два раза , то эти два числа нужно записать и в строке и в столбце, чтобы они участвовали в перемножениях найденных чисел по два раза.
То есть в центральной строке запишем:
4•2•9
В левый столбец запишем:
3
4
6
А в правый столбец запишем:
1
9
8
3 |_| 1
4 |2| 9
6 |_| 8
(Разумеется, в солбцах верхние и нижние числа можно менять местами.
Можно и столбцы поменять местами.
Важно, что в центре должно остаться число 2, и центральная строк, кроме 2, должна включать числа 4 и 9).
ПРОВЕРКА:
1) Произведение чисел в левом столбце:
3•4•6 = 72
2)Произведение чисел в правом столбце:
1•8•9 = 72
3) Произведение чисел в центральной строке:
4•2•9 = 72