Нужно провести нормаль к функции y=x^2-4х параллельно прямой х+2y+4=0 .Сделать чертеж . за

Пошаговое объяснение:

сперва перепишем х+2y+4=0 в виде уравнения с угловым коэффициентом

y = -0.5x-2

здесь коффициент угла наклона = -0,5

значит, у нашей нормали должен быть такой же коффициент угла наклона = -0,5

значит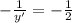     ⇒  y'(x₀)=2

y'(x) = 2x-4;   2x₀-4=2;   x₀ = 3;   у(х₀) = 3²-4*3=9-12 = -3

вот в этой точке (3; -3)и будет проходить нормаль к графику

а уравнение нормали

теперь проверим. напишем касательнуб в этой точке

и проверим, что они перепендикулярны

направляющий вектор нормали n₁ = (1; -05)

направляющий вектор касательной n₂ = (1; 2)

их скалярное произведение

a · b = ax · bx + ay · by = 1 · 1 + (-0.5) · 2 = 1 - 1 = 0

Так как скалярное произведение равно нулю, то эти векторы перпендикулярны

т.е. мы правильно  нашли точку и построили в ней нормаль параллельную х+2y+4=0