и если на сложно можно методом интервалов .
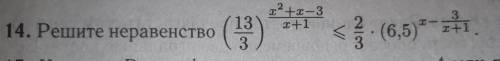
Другие вопросы по теме Математика
Популярные вопросы
- Разложите на множители выражения: 7)xy-x^2+3 (x-y) 8)q (n-c)-pn+pc...
3 - Изменить согласуя с числом.1 яблоко,2яблока,5 яблок, как правильно...
2 - Что бывает густое, существительные среднего рода...
1 - Книга никольский 9 класс номер 275 сопротивление цепи двух параллельно...
3 - Различить растворы сульфата натрия хлорид натрия и серной кислоты...
3 - Решите уравнение три целых две третьих минус х плюс одна третья...
3 - Вморе вышло 16 яхт больших а маленьких на7 меньше сколько всего...
1 - Выполнить морфологический разбор слов: утренней(зарею); выезжают...
2 - Какие вопросы мистер гринвуд задал своим ученикам? прочитай ответы,...
3 - Выполнить вычисление с обьяснением.32*3= + * =...
3
Пошаговое объяснение: ( ^ -знак степени)
(a/b)^x=a^x /b^x -формула(1), x -3/(x+1)=(x^2+x-3)/(x+1), т.е. показатели одинаковые, пусть (x^2 +x-3) /(x+1)=z, тогда (13/3) ^z <= 2/3*(13/2)^z
поделим обе части на (13/2^z, используя формулу (1), получим,
(2/3)^z <=2/3, т, к. основание < 1, то z>=1, обратная замена:
(x^2+x-3)/(x+1) >=1, (x^2+x-3-x-1) /(x+1) >=0, (x^2-4)/(x+1)>=0,
(x-2)(x+2)/(x+1)>=0, метод интервалов:
-___[-2]+(-1)-[2]+___ надо >=,
ответ: [-2;-1)u [2; +Беск.) ODЗ: х не = -1