Здравствуйте с задачами по геометрии.
1.Гора Эльбрус (на Кавказе) поднимается над уровнем моря на 5600м. Как далеко можно видеть с вершины этой горы?
2.М – наблюдательный пункт высотой h метров над Землей; радиус Земли R, MT = d есть наибольшее видимое расстояние. Доказать, что
3.Найти расстояние от острова, находящегося на озере, до пункта В на берегу. (Остров О принять за точку).
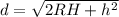
Другие вопросы по теме Геометрия
Популярные вопросы
- Чтение. Прочитайте в выполните задания. Промышленные роботы или...
3 - По моги те соч по английскому ...
1 - пожж если не ответите жалобу...
2 - 4 Cross out one extra word in each sentence. 1 It s a difficult...
3 - решит контрольную работу ...
1 - Тёмные сосульки свесали с крыш Залние все части речи...
2 - В равнобедренном треугольнике ABC величина угла при вершине B равна...
2 - یا ج م م ج + کد : 3 - 3 -% -ية 2 + 3 = 5- ( : ة+ 5 = 40 +15 - 55.=--=که...
1 - нужно у меня СОР Далеко на восточном краю Земли находился золотой...
1 - 4) Найти сумму кубов всех целых чисел от 20 до 40. Составьте: а)...
3
гипотенуза² = катет 1² + катет 2²
В данном случае, катет 1 - это высота горы Эльбрус (5600м), а катет 2 - это расстояние, которое мы хотим найти. Подставляя известные значения в формулу:
катет 2² = гипотенуза² - катет 1²
катет 2² = расстояние² - 5600²
Теперь мы можем подставить данное значение в формулу и решить ее:
катет 2² = расстояние² - 5600²
расстояние² = катет 2² + 5600²
расстояние² = катет 2² + 31360000
расстояние = √(катет 2² + 31360000)
Таким образом, расстояние, которое можно увидеть с вершины горы Эльбрус, равно корню квадратному (√) от суммы катета 2 в квадрате и 31360000.
2. Для доказательства данного утверждения мы можем использовать подобие треугольников. Если мы нарисуем прямую, проходящую через наблюдательный пункт М и касающуюся поверхности Земли T, а также проведем прямую от точки М до центра Земли O, то получим два подобных треугольника: MTO и MBO.
Так как треугольник MTO подобен треугольнику MBO, мы можем записать пропорцию соотношения их сторон:
MT/MB = TO/OB
MT - это наибольшее видимое расстояние, которое мы хотим найти. TO - это высота М над Землей (h), OB - это радиус Земли (R).
Теперь мы можем записать данную пропорцию и решить ее:
MT/MB = TO/OB
MT/R = h/(R-h)
Кросс-перемножим и решим полученное уравнение:
MT(R-h) = hR
MTR - MTh = hR
MTR = hR + MTh
MT = h + MT(h/R)
Таким образом, наибольшее видимое расстояние MT равно сумме высоты М над Землей h и произведения MT на отношение h к R.
3. Чтобы найти расстояние от острова до пункта В на берегу, мы можем применить теорему Пифагора к треугольнику, образованному островом О, пунктом А на озере и пунктом В на берегу.
В данном случае, расстояние от острова до пункта В - это гипотенуза треугольника, а расстояние от острова до пункта А и расстояние от пункта А до пункта В - это катеты. Мы можем записать уравнение:
расстояние от острова до пункта В² = расстояние от острова до пункта А² + расстояние от пункта А до пункта В²
Теперь мы можем подставить известные значения и решить уравнение:
расстояние от острова до пункта В² = 10² + 15²
расстояние от острова до пункта В² = 100 + 225
расстояние от острова до пункта В = √325
Таким образом, расстояние от острова до пункта В на берегу равно корню квадратному (√) от суммы катета 1 в квадрате (10²) и катета 2 в квадрате (15²).