Впрямоугольном треугольнике авс угол с=90 градусов медианы пересекаются в точке о ов=10см вс=12 найдите гипотенузу

Медианы в точке пересечения деляться в отношении 2:1 начиная с вершины..

1) во=10, тогда вв1(медиана)=15

2) по т. Пифогора, в1с=√225-144= √81=9

3) т.к. вв1 медиана, то ав1=в1с, то ас=18

4) по т. Пифогора, ав=√144+324=√468=6√13 

ответ: 6√13

пс: я не уверена в последнем действии 

медианы в треугольниках пересекаюстся в точке о и делятся в соотношении 1:2.

следовательно медиана выходящая из угла В (назовем ее ВН) = 15.

СН^2=HB^2-CB^2=15^2-12^2=225-144=81. CH=9.

СН- половина АС, т.к. медиана падая на сторону делит ее пополам.

Значит АС=18.

Отсюда найдем АВ по теореме Пифагора. 

AB^2=AC^2+CB^2=18^2+12^2=324+144=468.

AB=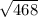 =