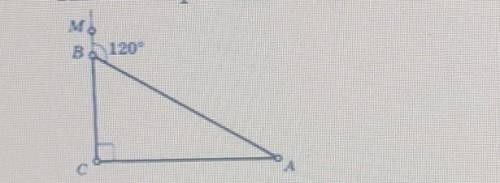
В прямоугольном треугольнике АВС угол С=90°, угол МВА=120°,АВ+ВС=36см. Найти стороны AB и ВС
, ответ должен быть в виде уравнения
Другие вопросы по теме Геометрия
Популярные вопросы
- Выражение ctg a +tg(90°+a)+ cos(180°-a) заранее)...
2 - Распредели примеры в группы,обозначенные цифрами,,: 1 однородные...
1 - Заранее ! №30 вставьте пропущенные слова . большинство клеток...
3 - Частица массой 0.001 мг имеющая заряд 1 мккл влетает со скоростью...
2 - Тигр бежит со скоростью 1км/мин, а лев-со скоростью 1300м/мин....
1 - Правильно написать предложение( расставить разные знаки ): им...
1 - Начертить прямоугольник4см а ширинав4 разаменьше найти периметр...
3 - Выручка 100000 средняя стоимость еденицы920 руб средний чек...
1 - Сведения которые можно собирать хранить передавать обрабатывать...
2 - Какое проверочное слово к слову милиционер...
3
Первым шагом разберемся с углом МВА, который равен 120°. Угол МВА - это угол, образованный гипотенузой треугольника (АВ) и высотой, опущенной из вершины А (БН). Так как у нас прямоугольный треугольник, то угол МВА является дополнительным к углу С, то есть 180° - 90° = 90°. Значит, угол МВА равен 90°.
В прямоугольном треугольнике один из углов всегда равен 90°. Так как угол С = 90°, то второй угол (в данном случае МВА) также равен 90°. Это значит, что треугольник АВС является прямоугольным при вершине А.
Теперь перейдем к нахождению сторон АВ и ВС.
Для нахождения стороны АВ мы можем использовать теорему Пифагора, так как треугольник АВС является прямоугольным. Согласно теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы. В нашем случае, АВ - это гипотенуза, ВС и АС - это катеты.
У нас уже известно, что АВ + ВС = 36 см. Пусть ВС = а, тогда АВ = 36 - а.
Применим теорему Пифагора:
(36 - а)^2 = (а)^2 + (АС)^2
Раскроем скобки:
1296 - 72а + а^2 = а^2 + (АС)^2
Уберем а^2 из обеих частей:
1296 - 72а = (АС)^2
Выражение (АС)^2 означает квадрат стороны АС.
Затем решим это уравнение, чтобы найти значение а:
1296 - 72а = (АС)^2
72а = 1296 - (АС)^2
а = (1296 - (АС)^2)/72
Теперь мы знаем значение а и можем найти стороны АВ и ВС:
АВ = 36 - а
ВС = а
Таким образом, ответом на вопрос являются уравнения:
АВ = 36 - ((1296 - (АС)^2)/72)
ВС = (1296 - (АС)^2)/72