1. Геометрия
  2. В прямоугольном параллелепипеде

В прямоугольном параллелепипеде ABCDA1B1C1D1AB=1, DD1=2, A1D1=2 Найдете AC1.

ЕваКимСокДжин ЕваКимСокДжин    3   18.06.2020 11:25    2

Ответы
vyrov08 vyrov08  15.10.2020 14:22
Дано:

Прямоугольный параллелепиппед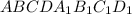 ABCDA_1B_1C_1D_1

AB = 1

DD1 = 2

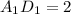
A_1D_1 = 2

Найти: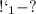

АС_1 - ?

Решение:

АС_1 - диагональ данного прямоугольного параллелепиппеда.

Квадрат диагонали прямоугольного параллелепиппеда равен сумме квадратов его 3 измерений: (d = √(a² + b² + c²), где d - диагональ прямоугольного параллелепиппеда; а, b, c - 3 измерения прямоугольного параллелепиппеда)

а, b, c - AB, A1D1, DD1.

d - AC1.

\Rightarrow d = AC_1 = \sqrt{AB^2 + A_1D_1 \: ^2 + DD_1 \: ^2} = \sqrt{1^2 + 2^2 + 2^2}= \sqrt{9} = 3

Итак, АС1 = 3

Задача решена! ☑

ответ: \Large{\boxed{3}}
В прямоугольном параллелепипеде ABCDA1B1C1D1AB=1, DD1=2, A1D1=2 Найдете AC1.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
denthegamerp01iih denthegamerp01iih  25.07.2019 00:00
Один из углов прямоугольного треугольника равен 60 градусов, а сумма гипотенузы и меньшего катета 18 см. найти гипотенузу и катет, можно с дано и решением...
minis551 minis551  25.07.2019 00:00
Втреугольнике авс угол с равен 90 градусов,ав=10,sina=0,9.найдите вс....
violakim2806 violakim2806  24.10.2019 12:27
Одна сторона треугольника на 3 см меньше другой а угол между ними 60 найдите периметр треугольника если его третья сторона равна 7...
vladyulin vladyulin  24.10.2019 12:24
Ak bf медианы треугольника abc bf=36 найдите длину отрезка mf​...
хлюпхлюпик хлюпхлюпик  24.10.2019 12:21
4. дан тупой угол аов и точка c, лежащая в его внутренней оолаи1) постройте луч od проходящий через точку си лежащий внутри угла aob2) запишите, чему равна величина угла аов3)...
blablabla114 blablabla114  24.10.2019 12:21
Сторона ав треугольника вас равна 15 см. сторона км разделена на 3 равные части и через точки деления проведены прямые, паралельные стороны вс. найдите блины отрезков этих прямых,...
ручка41 ручка41  24.10.2019 12:19
Основа прямої призми – прямокутна трапеція, більша бічна сторона якої дорівнює більшій основі і має довжину 25 см, а висота трапеції – 24 см. бічне ребро призми дорівнює 20 см....
Varbax896 Varbax896  24.10.2019 12:18
Хелп вариант 2. решите треугольник1) а = 5, c = 9, а = 42°.2) b = 7, с = 12, b = 279, 90° 3) а = 13, c = 14, b = 121°.4) а = 8, а = 27°, b = 54°.| 5) а = 7, b = 8, с = 12.​...
akjol21 akjol21  24.10.2019 12:17
Задання суммативного оценивания за 1-четверть по 7 класс вариант-1. даны отрелки ab. точка е, не лежащая на прямой ab, и точка c, лежащая на прямой ab какое вареноерасположение...
darya4ern1 darya4ern1  24.10.2019 12:17
Углы треугольника равны 40°,70°,70°.найдите все 6 углов ,которые образуются при пересечении высот данного треугольника​...

Популярные вопросы