В параллелограмме M
N
K
T
MNKT точка
Q
Q делит сторону
T
K
TK так, что
T
Q
:
Q
K
=
1
:
3
TQ:QK=1:3. Найди стороны треугольника
Q
K
L
QKL, если
M
Q
=
22
MQ=22,
M
T
=
20
MT=20,
T
Q
=
5
TQ=5.
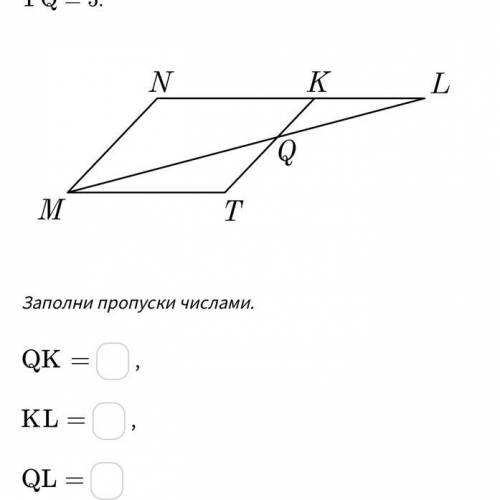
Другие вопросы по теме Геометрия
Популярные вопросы
- Фермер собрал 740 ц моркови,а свеклы-на 380 ц больше.сколько центнеров свёклы...
1 - Вычисли объем воды которую необходими выпарить из 200 кг60 % серной кислоты...
1 - Сдвух станций,расстояние между которыми 720 км,вышли одновременно на встречу...
2 - Вокружности с центром о проведена хорда ав. отрезок ос-радиус окружности, перпендикулярный...
3 - Краткое сочинение не болия 4 5 предложений на тему дельфины (пример дельфины...
2 - 1. сторона ab треугольника abc равна 8 см. 1) a = 30градусам ,...
3 - Сократите дробь: (x+корень из x)/x-1...
2 - Стороны параллелограмма 6см и 5см, а один из углов равен 150градусов.найдите...
3 - Найдите какое-нибудь натуральное число n, чтобы число 2^n + 15 было составным....
3 - Вшкольном оркестре 7 девачек а мальчиков в 4 раза больше чем девочек сколько...
2
По условию, известно, что отношение длин сторон TQ и QK равно 1:3. Пусть длина стороны TQ равна x. Тогда длина стороны QK будет равна 3x, так как отношение равно 1:3.
Также по условию дано, что MQ равна 22, MT равна 20 и TQ равна 5.
Так как МТ является диагональю параллелограмма, то MT равна длине диагонали КN. Также диагонали параллелограмма делятся пополам. Поэтому длина NK будет равна MT/2 = 20/2 = 10.
Теперь у нас есть все необходимые данные для нахождения сторон треугольника QKL.
Длина стороны KL будет равна сумме длин стороны QK и NK. Значит, KL = 3x + 10.
Длина стороны QL будет равна сумме длин стороны TQ и TK. Значит, QL = x + 5.
Длина стороны QK уже известна и равна 3x.
Таким образом, стороны треугольника QKL будут иметь следующие длины:
KL = 3x + 10,
QL = x + 5,
QK = 3x.
Осталось только найти значение x.
Из условия задачи мы знаем, что отношение длин сторон TQ и QK равно 1:3. Значит, TQ/QK = 1/3.
Мы также знаем, что TQ = 5 и QK = 3x. Подставив эти значения в уравнение, получим:
5/(3x) = 1/3.
Решим это уравнение:
Умножим обе части уравнения на 3x:
5 = x.
Таким образом, значение x равно 5.
Подставим это значение обратно в формулы для сторон треугольника QKL:
KL = 3x + 10 = 3 * 5 + 10 = 15 + 10 = 25,
QL = x + 5 = 5 + 5 = 10,
QK = 3x = 3 * 5 = 15.
Итак, стороны треугольника QKL равны:
KL = 25,
QL = 10,
QK = 15.