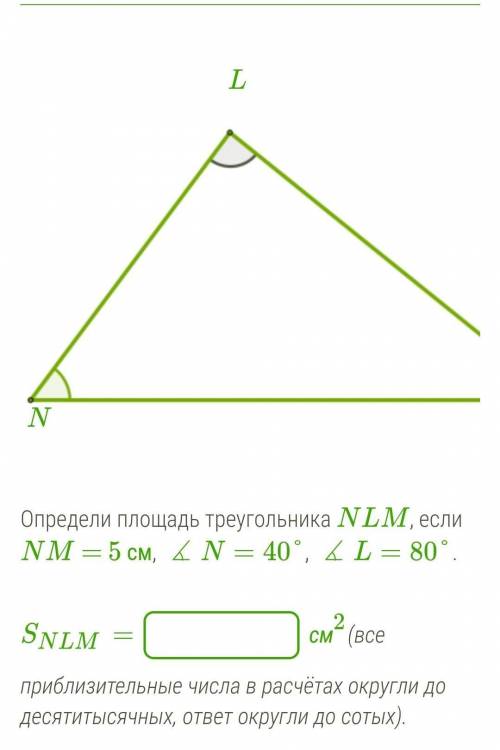
Определи площадь треугольника NLM, если NM = 5 см, ∡N=40°, ∡L=80°. SNLM= см2(все приблизительные числа в расчётах округли до десятитысячных, ответ округли до сотых).

Для определения площади треугольника NLM, мы можем использовать формулу площади треугольника, которая выглядит следующим образом:

S = (1/2) * a * b * sin(θ),

где S - площадь треугольника, a и b - две стороны треугольника, θ - угол между этими сторонами.

В данном случае, у нас есть сторона NM длиной 5 см и мы должны определить площадь треугольника NLM, зная два угла ∡N и ∡L.

1. Сначала найдем третий угол ∡M в треугольнике, используя свойство суммы углов в треугольнике. Сумма всех углов в треугольнике равна 180°, поэтому:

∡M = 180° - ∡N - ∡L
= 180° - 40° - 80°
= 60°.

Теперь у нас есть все три угла треугольника NLM.

2. Затем мы можем использовать закон синусов для определения стороны ML треугольника:

ML / sin(∡M) = NM / sin(∡N),
ML / sin(60°) = 5 / sin(40°).

Мы знаем, что sin(60°) ≈ 0,8660 и sin(40°) ≈ 0,6428, поэтому:

ML / 0,8660 = 5 / 0,6428,
ML ≈ (5 * 0,8660) / 0,6428,
ML ≈ 6,8304 / 0,6428,
ML ≈ 10,62 см.

Таким образом, сторона ML равна примерно 10,62 см.

3. Теперь, используя найденные значения сторон NM (5 см) и ML (примерно 10,62 см), и угол ∡N (40°), мы можем найти площадь треугольника NLM, используя формулу площади треугольника:

S = (1/2) * NM * ML * sin(∡N),
S ≈ (1/2) * 5 * 10,62 * sin(40°).

Мы знаем, что sin(40°) ≈ 0,6428, поэтому:

S ≈ (1/2) * 5 * 10,62 * 0,6428,
S ≈ 33,55 * 0,6428,
S ≈ 21,57354.

Округлим ответ до сотых:

S ≈ 21,57 см².

Таким образом, площадь треугольника NLM приближенно равна 21,57 см².