Найти уравнение прямой, проходящей через точку a(9; -12) и перпендикулярно к прямой, соединяющий точки b(2; -4) и c(3; -1).

Найдем уравнение для 2 прямой по формуле y=kx+b

Значит уравнение для 2 прямой: y=3x-10

Т. к.  2 прямая перпендикулярна к 1, то угловой коэффициент 1 прямой обратно пропорционален, т. е.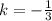 . Но она же должна проходить через точку А(9;-12), тогда:

Тогда уравнение первой прямой будет выглядеть так: