Найдите диагонали параллелограмма площадью 96√2 см, если одна из них на 8 см длиннее другой, а угол между ними 45 °
знайдіть діагоналі паралелограма площею 96√2 см², якщо одна з них на 8 см довша за другу, а кут між ними 45°
Другие вопросы по теме Геометрия
Популярные вопросы
- Ab=10cm bc=15cm угл abc=150° найти s-?...
2 - (12y+18)(1,6-0,2y)=0 решите понятно...
1 - Скаким периодом должна вращаться карусель, если частота ее вращения...
2 - Врезультате а-распада ядро изотопа полония превращается в ядро изотопа:...
3 - Рассчитайте обьем (н.у) ацителена, который модно получить из 20г технического...
1 - 1. сформулируйте смысл понятия взаимодействие тел . в чем заключается...
1 - На сколько надо умножить 2 чтоб стало корень из...
1 - Найдите область определения функции: f(x)=log0,1(0,01-x^2)...
3 - Решите логарифмическое уравнение: log0,2(x+4)+log0,2(x-7)=log0,2(7-x)...
1 - Найти производную функции у=2х^2/1-7х...
1
16 см; 24 см.
Объяснение:
Площадь параллелограмма вычисляется по формуле:
где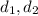 - диагонали параллелограмма, α - угол между диагоналями.
- диагонали параллелограмма, α - угол между диагоналями.
Подставляем в эту формулу известные данные и выражаем произведение диагоналей.
Пусть d₁ = x см, тогда d₂ = (х+8) см.
d₁ * d₂ = 384.
Составим уравнение.
d₁ = x = 16 (см)
d₂ = (х+8) = 16+8 = 24 (см).