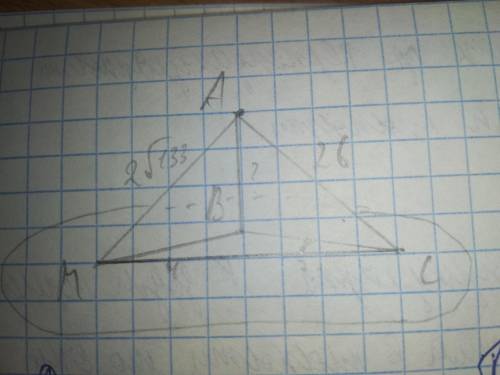
Дано:
MA=2√133 см
AC=26 см
MB:BC=5:4
Найти: AB

Для решения данной задачи, мы будем использовать теорему Пифагора, а также соотношение между сегментами, проходящими от вершины прямого угла до основания прямоугольного треугольника.

Известно, что MA = 2√133 см и AC = 26 см. Мы можем использовать теорему Пифагора для поиска длины AB.

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. В данном случае, AB является гипотенузой, поэтому мы можем записать уравнение следующим образом:

AB² = MB² + MA²

Теперь, нам необходимо найти длины MB и BC. Дано, что отношение MB к BC равно 5:4. Мы можем представить это отношение как следующую пропорцию:

MB / BC = 5 / 4

После умножения обеих сторон на 4, получаем:

4 * MB = 5 * BC

Теперь, чтобы найти длину BC, мы можем разделить длину MB на 4.

Длина BC = MB / 4

Из геометрии известно, что AC является высотой прямоугольного треугольника. Мы можем использовать это знание, чтобы записать следующую пропорцию:

AC / BC = MA / MB

После умножения обеих сторон на BC, получаем:

AC * BC = MA * MB

Теперь мы можем заменить значение BC на MB / 4 и решить уравнение относительно MB.

AC * (MB / 4) = MA * MB

После умножения обеих частей уравнения на 4, получаем:

AC * MB = 4 * MA * MB

Теперь, чтобы найти значение MB, мы можем делить обе части уравнения на AC.

MB = (4 * MA * MB) / AC

Используя данные из условия задачи, мы можем подставить значения в уравнение и решить его:

MB = (4 * 2√133 * MB) / 26

26 * MB = 8√133 * MB

После деления обеих частей уравнения на MB и упрощения, получаем:

26 = 8√133

√133 = 26 / 8

√133 = 13 / 4

Теперь, мы можем найти длину BC, используя значение MB:

BC = MB / 4 = (13 / 4) / 4 = 13 / 16

Наконец, мы можем подставить значения MA, AC и BC в уравнение для нахождения длины AB:

AB² = MB² + MA² = BC² + AC²

AB² = (13 / 16)² + 26²

AB² = (13² / 16²) + 26²

AB² = 169 / 256 + 676

AB² = 169 / 256 + 676 * (256 / 256)

AB² = 169 / 256 + 173056 / 256

AB² = 173225 / 256

AB = √(173225 / 256)

AB = √173225 / √256

AB = 415 / 16

Длина AB равна 415 / 16 см.