Дано: A//B
Угол 1 + угол 2 =160
Найти угол1,2,3,4,5,6
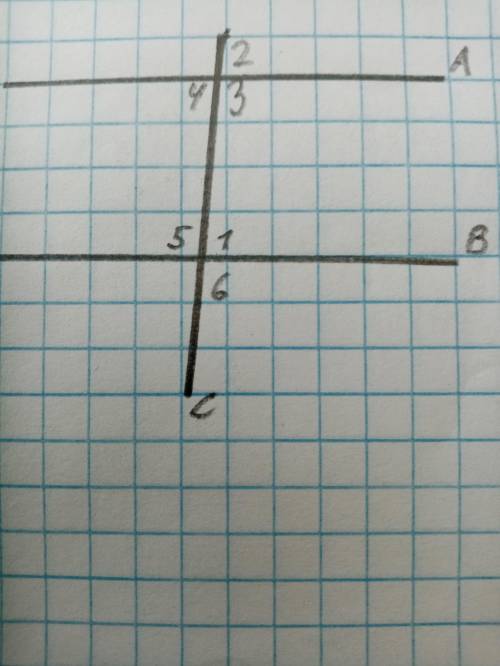
Другие вопросы по теме Геометрия
Популярные вопросы
- Отзыв по сказке а.с.пушкин дубровский...
1 - Напишите в следующих двойных неравевенствах вместо неизвестного такое...
2 - Сколько страниц сказка о царе салтане а с пушкин...
2 - Отзыв по сказке а.с.пушкин барышня-крестьянка ....
2 - Как изменяется климат в россии с запада на восток , с севера на юг....
1 - Прочитайте ниже текст, в котором пропущен ряд слов. выберите из предлагаемого...
3 - Пп бажов серебреное копытце герои и сколько страниц...
2 - Записки охотника тургенев о чем говориться в произведении? не кратко...
3 - Один з коренів рівняння х² + 4x + q = 0 дорівнює -6. знайдіть q і інший...
2 - Сжатый пересказ уроки французского (5-7 предложений) заранее...
3
Изображение, которое дано, показывает две параллельные прямые A и B. Угол 1 и угол 2 образованы пересекающимися прямыми и являются внутренними углами. Из условия задачи, мы знаем, что сумма угла 1 и угла 2 равна 160 градусам.
1. Уголи 1 и 2 являются соответственными углами, так как они образуются пересекающимися прямыми A и B и параллельными прямыми. Поэтому, угол 1 и угол 3 также являются соответственными углами, и их сумма равна 180 градусам.
Угол 1 + угол 3 = 180 градусов.
2. Угол 2 и угол 4 также являются соответственными углами, и их сумма также равна 180 градусам.
Угол 2 + угол 4 = 180 градусов.
Теперь, у нас есть система уравнений:
Угол 1 + угол 3 = 180 градусов (уравнение 1)
Угол 2 + угол 4 = 180 градусов (уравнение 2)
Угол 1 + угол 2 = 160 градусов (уравнение 3)
Мы можем решить эту систему уравнений, используя метод подстановки или метод сложения/вычитания.
Давайте решим эту систему уравнений, используя метод подстановки:
Из уравнения 3 выразим угол 1 через угол 2:
Угол 1 = 160 - угол 2
Подставим это значение угла 1 в уравнение 1:
(160 - угол 2) + угол 3 = 180
Раскроем скобки и проведем преобразования:
160 - угол 2 + угол 3 = 180
- угол 2 + угол 3 = 180 - 160
- угол 2 + угол 3 = 20
Аналогично, из уравнения 3, выразим угол 2 через угол 1:
Угол 2 = 160 - угол 1
Подставим это значение угла 2 в уравнение 2:
(160 - угол 1) + угол 4 = 180
Раскроем скобки и проведем преобразования:
160 - угол 1 + угол 4 = 180
- угол 1 + угол 4 = 180 - 160
- угол 1 + угол 4 = 20
Теперь, у нас есть два уравнения:
- угол 2 + угол 3 = 20 (уравнение 4)
- угол 1 + угол 4 = 20 (уравнение 5)
Мы можем решить эту систему уравнений, используя метод сложения/вычитания. Просуммируем уравнения 4 и 5:
(- угол 2 + угол 3) + (- угол 1 + угол 4) = 20 + 20
- угол 2 - угол 1 + угол 3 + угол 4 = 40
Заметим, что угол 3 и угол 4 являются смежными углами, так как они образованы пересекающимися прямыми A и B. Из свойства смежных углов, мы знаем, что их сумма равна 180 градусам. Поэтому, угол 3 + угол 4 = 180.
Подставим это значение в уравнение:
- угол 2 - угол 1 + 180 = 40
Перегруппируем и проведем преобразования:
- угол 2 - угол 1 = 40 - 180
- угол 2 - угол 1 = -140
Теперь, у нас есть два уравнения:
- угол 2 - угол 1 = -140 (уравнение 6)
- угол 2 + угол 3 = 20 (уравнение 4)
Мы можем решить эту систему уравнений, вычитая уравнение 6 из уравнения 4:
- угол 2 + угол 3 - (- угол 2 + угол 1) = 20 - (-140)
2 угол 2 + угол 3 + угол 1 = 20 + 140
2 угол 2 + угол 3 + угол 1 = 160
Теперь, у нас есть два уравнения:
2 угол 2 + угол 3 + угол 1 = 160 (уравнение 7)
- угол 2 - угол 1 = -140 (уравнение 6)
Мы можем решить эту систему уравнений, используя метод сложения/вычитания. Просуммируем уравнения 6 и 7:
(2 угол 2 + угол 3 + угол 1) + (- угол 2 - угол 1) = 160 + (-140)
2 угол 2 - угол 2 + угол 3 - угол 1 = 160 - 140
угол 2 + угол 3 - угол 1 = 20
Теперь, у нас есть одно уравнение:
угол 2 + угол 3 - угол 1 = 20 (уравнение 8)
Мы знаем, что сумма угла 2, угла 3 и угла 4 равна 180 градусам. Из уравнений 8 и 5, мы можем выразить угол 3 через угол 2 и угол 1:
угол 3 = 20 + угол 1 - угол 2
Теперь, у нас есть выражение для угла 3 через угол 2 и угол 1.
Для нахождения остальных углов, нам нужно использовать свойства параллельных прямых. Изображение показывает, что две параллельные прямые пересекаются третьей прямой (здесь обозначена точкой O). В точке O, образуются две вертикальные углы (угол 5 и угол 6), которые являются равными.
Таким образом, угол 3 и угол 5 равны:
угол 3 = угол 5.
Из уравнения 3, мы можем выразить угол 5 через угол 1:
угол 5 = угол 1
Теперь, у нас есть выражение для угла 5 через угол 1.
Из уравнения 1, мы также можем выразить угол 6 через угол 3:
угол 6 = 180 - угол 3
Теперь, у нас есть выражение для угла 6 через угол 3.
Таким образом, чтобы найти угол 1, угол 2, угол 3, угол 4, угол 5 и угол 6, мы можем использовать следующие выражения:
угол 1 = 160 - угол 2
угол 2 - угол 1 = -140
угол 2 + угол 3 - угол 1 = 20
угол 3 = 20 + угол 1 - угол 2
угол 3 = угол 5
угол 5 = угол 1
угол 6 = 180 - угол 3
Таким образом, ответ на вопрос будет следующим:
угол 1 = 160 - угол 2
угол 2 - угол 1 = -140
угол 2 + угол 3 - угол 1 = 20
угол 3 = 20 + угол 1 - угол 2
угол 4 = 180 - угол 2
угол 5 = угол 1
угол 6 = 180 - угол 3.
Все эти углы можно найти, заменяя значениями угла 1 или угла 2 и решая получившиеся уравнения и выражения.