Большее основание равнобедренной трапеции, принадлежит плоскости а, которая с плоскостью трапеции образует угол 60°. Зная, что основания трапеции 15 см и 5 см, а боковая сторона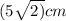
,найти расстояние между меньшим основанием и плоскостью альфа и угол между диагональю трапеции и плоскостью
можно с чертежом ​

5 вроде                    да я уверен на 100№

                         

Добрый день!

Давайте разберемся с данным вопросом шаг за шагом.

1. Начнем с построения. Нарисуем прямоугольную систему координат с плоскостью альфа, параллельной оси x, и плоскостью трапеции, параллельной плоскости x-y.

2. Обозначим точками A и B основания трапеции, эти точки будут находиться на оси x. По условию, длина большего основания AB равна 15 см, а длина меньшего основания CD равна 5 см.

3. Поскольку трапеция равнобедренная, то диагонали CE и DF будут равны между собой и делить основания трапеции пополам. Длина диагоналей равна половине суммы оснований: CE = DF = (AB + CD) / 2 = (15 + 5) / 2 = 10 / 2 = 5 см.

4. Так как плоскость альфа и плоскость трапеции образуют угол 60°, то у нас есть правильный треугольник ACE, где AC - это одна из диагоналей трапеции, а CE - боковая сторона равнобедренной трапеции. Также дано, что CE = (5√2) см.

5. Чтобы найти расстояние между меньшим основанием CD и плоскостью альфа, нам нужно найти отрезок CR, где R - проекция точки C на плоскость альфа. Очевидно, что угол между отрезком CR и прямой AC будет прямым, так как они находятся на плоскости альфа.

6. Введем вектора AC и CE согласно прямоугольной системе координат. Обозначим вектор AC как a и вектор CE как b. Зная длины AC и CE, мы можем записать их вектора в виде a = (15, 0, 0) и b = (5√2, 0, 0).

7. Теперь нам нужно найти координаты вектора CR. Так как угол между векторами AC и CR прямой, мы можем воспользоваться достаточно простым подходом. Поскольку AC и CR перпендикулярны друг другу, их скалярное произведение равно нулю. То есть, a · CR = 0.

8. Определим вектор CR как (x, y, z). Тогда a · CR = (15, 0, 0) · (x, y, z) = 15x + 0y + 0z = 15x = 0.

9. Из уравнения 15x = 0 следует, что x равно нулю. Значит, координаты вектора CR будут (0, y, z).

10. Также мы знаем, что направляющий вектор плоскости альфа совпадает с нормалью вектора CR. Вектор нормали к плоскости альфа будет иметь вид (0, a, b), где a и b - некие числа.

11. Теперь найдем векторное произведение вектора CR и вектора нормали к плоскости альфа. Результатом векторного произведения будет вектор, перпендикулярный обоим входным векторам и, следовательно, лежащий на плоскости альфа.

12. Создадим уравнение для векторного произведения CR и (0, a, b) и найдем его. Запишем уравнение векторного произведения CR и (0, a, b):

(0, y, z) × (0, a, b) = (bz - ay, -bz, ay).

13. По условию известно, что такой вектор лежит на плоскости альфа, мы можем приравнять его к вектору нормали плоскости альфа (0, a, b) и найти соответствующие значения для y и z. Запишем уравнение:

(bz - ay, -bz, ay) = (0, a, b).

14. Сравним компоненты левой и правой сторон уравнения:

bz - ay = 0 --> bz = ay,
-bz = a,
ay = b.

15. Зная, что a ≠ 0, b ≠ 0, мы можем решить эту систему уравнений. Из второго уравнения получаем, что bz = -a. Подставим это значение в первое уравнение:

-ay = -a --> y = 1.

16. Теперь найдем z, используя второе и третье уравнения:

b = a,
a = b.

17. Зная, что a = b, мы можем сделать вывод, что вектор CR будет выглядеть следующим образом: (0, 1, 1).

18. Итак, мы нашли вектор CR, который параллелен плоскости альфа и соединяет точку C с точкой R (проекцией точки C на плоскость альфа). Координаты вектора CR равны (0, 1, 1).

19. Расстояние между меньшим основанием CD и плоскостью альфа равно длине проекции отрезка CR на ось x. Длина этой проекции будет равна координате x вектора CR: 0 см.

20. Значит, расстояние между меньшим основанием CD и плоскостью альфа равно 0 см.

21. Наконец, угол между диагональю трапеции и плоскостью альфа будет равен углу между векторами AC и CR. Используем формулу для нахождения косинуса угла между векторами: cos θ = (AC · CR) / (|AC| |CR|).

22. В нашем случае вектор AC - это вектор a = (15, 0, 0), а вектор CR - это вектор (0, 1, 1). Используя формулу, мы получаем: cos θ = (15*0 + 0*1 + 0*1) / (√(15^2 + 0^2 + 0^2) * √(0^2 + 1^2 + 1^2)) = 0 / (√(225 + 0 + 0) * √(0 + 1 + 1)) = 0 / (√225 * √2) = 0 / 15√2 = 0.

23. Значит, угол между диагональю трапеции и плоскостью альфа равен 0°.

Надеюсь, этот подробный ответ помог вам понять решение и решить данную задачу. Если у вас возникнут еще какие-либо вопросы, не стесняйтесь задавать их!