1. Внешний угол при основании равнобедренного треугольника равен 140 Найти углы треугольника.
2. В треугольнике ABC угол А в 4 раза меньше угла В, аутопс на 90
меньше угла В.
а) Найти углы треугольника ABC.
б) Сравнить стороны AB и BC.
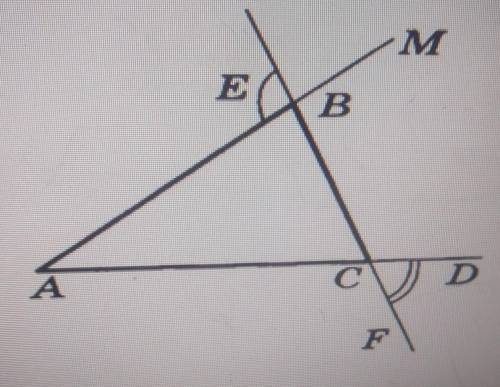
3. На рисунке. Найдите сторону АВ треугольника АВС
Другие вопросы по теме Геометрия
Популярные вопросы
- Скласти сенкан азік Азімов...
2 - В чём величие писателя А.И.Солженицына?...
2 - Верны ли следующие суждения о роли государства в современной экономике: А)...
2 - Переведите 12км 476 м 8дм 5 см в десятичную дробь...
2 - 10. Продукты взаимодействия соляной кислоты и оксида меди(II) а) CuCl2 +...
2 - Символом чего является стихотворение железная дорога символом будущего настоящего...
3 - Бетонную балку массой 2 т равномерно подняли на высоту 5 м, совершив для...
2 - Сделать выводы: - Какова тематика и проблематика рассказа Горького? - Над...
3 - ZAOB = 52°, ZBOC = 18° және OB сәулесі ортақ, АОС бұрышының шамасын тап.Жауабы:...
3 - 5. Какой в основном рельеф Северной Европы? ...
3
Внешний угол при основании равнобедренного треугольника равен сумме двух других углов треугольника.
Пусть углы равнобедренного треугольника обозначены как A, B и C, где углы A и B равны, а угол C - внешний угол при основании. Тогда мы знаем, что угол C = 140 градусов.
Следовательно, углы A и B будут равны половине разности 180 градусов и угла C.
A = B = (180 - C)/2 = (180 - 140)/2 = 40/2 = 20 градусов.
Ответ: углы треугольника равны 20 градусов.
2. а) Для решения этой задачи мы воспользуемся свойством суммы углов треугольника и информацией о соотношении углов.
Пусть углы треугольника обозначены как А, В и С, где угол А в 4 раза меньше угла В, а угол С - внешний угол на 90 градусов меньше угла В. Тогда у нас есть два уравнения:
А = В/4 (1)
С = В - 90 (2)
Мы можем использовать первое уравнение, чтобы выразить А через В и затем подставить это значение во второе уравнение:
А = В/4
В = 4А
Теперь подставим значение В во второе уравнение:
С = 4А - 90
Нам нужно найти значения всех трех углов треугольника ABC. Для этого сумма всех углов треугольника должна быть равна 180 градусов:
А + В + С = 180
Теперь мы можем подставить значения А и С из предыдущих уравнений и решить уравнение:
А + В + С = 180
А + 4А + 4А - 90 = 180
9А - 90 = 180
9А = 270
А = 30
Теперь мы можем найти значения В и С, подставив значение А в уравнения (1) и (2):
В = 4А = 4*30 = 120
С = 4А - 90 = 4*30 - 90 = 120 - 90 = 30
Ответ: углы треугольника равны А = 30 градусов, В = 120 градусов, С = 30 градусов.
б) Чтобы сравнить стороны AB и BC, мы можем использовать свойства равнобедренного треугольника.
Равнобедренный треугольник имеет две равные стороны и два равных угла напротив этих сторон. Мы знаем, что углы А и В равны, поэтому стороны AB и BC должны быть равны.
Ответ: стороны AB и BC равны.
3. Для нахождения стороны АВ треугольника АВС, мы можем использовать теорему Пифагора.
Согласно теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
На рисунке дан прямоугольный треугольник АВС, где угол АВС - прямой угол, и известны длины сторон AC и CB.
Мы должны найти длину стороны АВ.
Пусть АВ = x. Тогда мы можем записать следующее уравнение:
AC^2 + CB^2 = AB^2
Подставим известные значения:
10^2 + x^2 = 20^2
100 + x^2 = 400
x^2 = 400 - 100
x^2 = 300
x = √300
Ответ: сторона АВ треугольника АВС равна √300.