Выяснить, при каком значении а многочлен P(х) делится на многочлен Q(х) P(х)= -4х^2+ах+5, Q(х)= 4х+5
Другие вопросы по теме Алгебра
Популярные вопросы
- Ask questions for these answers. use the words in brackets. 1.how tall is your...
2 - 1. с данными корнями образуйте глаголы неопределённой формы при суффиксов -а-...
3 - Не вычесляя найди одинаковые суммы вычесли все восемь сумм составь и запиши еще...
2 - She was glad to see me because i was english and she knew (little, few, a little)...
1 - Работа в театре с её людностью и горько-сладкой отрадой то полнила,то опустошала!...
2 - Напишите страшные на ночь хэллоуина, 10-12 предложений!...
1 - Вшкольной библиотеке на каждом стеллаже стоит одинаковое количество книг.в хранилище...
3 - Юбка родителный падеж поставить нужно...
1 - Напиши десять слов с безударной гласной...
3 - Собраный урожай яблок распределили следующим образом: 75% всех яблок заселили...
3
ответ: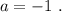
Воспользуемся теоремой Безу: остаток от деления многочлена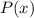 на двучлен
на двучлен 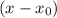 равен
равен 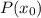 .
.
Тогда число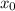 - корень многочлена
- корень многочлена 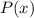 тогда и только тогда, когда P(x) делится без остатка на двучлен
тогда и только тогда, когда P(x) делится без остатка на двучлен 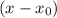 .
.
или