Вычислите площадь фигуры, ограниченной линиями:
. 1) у = х2 – 2х + 3, y = 0, х = 1, x = 2;
Другие вопросы по теме Алгебра
Популярные вопросы
- Моток веревки длиной 315 м разрезали на три части причём первая...
3 - Как умереть не мучительно но быстро?...
3 - 1. Предложение на рынке автомобильного топлива в разных странах...
3 - Поступки каких известных русских поэтов и писателей на ваш взгляд...
3 - С АРТИКЛЯМИ (Рашн стьюденс запутался) >...
2 - Выберите из предложенных в фото...
2 - с вопросами рассказ набокова Лебеда .1Назовите фамилию путиного...
1 - -поміж двох поданих словосполучень записати правильно побудоване...
2 - На упаковке зарядного устройства имеется надпись, гараар 0что выходное...
2 - 5.Визначте стилістичні умови використання та значення (відтінки...
3
ответ: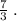
Объяснение:
ответ и решение во вложении