1. Алгебра
  2. Розв яжіть нерівність x^{2}+2^{log_{2}(-2x)}-15

Розв'яжіть нерівність x^{2}+2^{log_{2}(-2x)}-15< 0. у відповідь запишіть суму всіх розв'язків цієї нерівності.

софа336 софа336    3   24.09.2019 13:00    0

Ответы
ladybutiyarowa ladybutiyarowa  08.10.2020 15:19
Найдем сначала ОДЗ:-2x>0;x<0;
x^{2} + 2^{log_{2}(-2x)} -15\ \textless \ 0 \\ 2^{log_{2}(-2x)}=-2x \\ &#10;x^{2} -2x -15\ \textless \ 0 \\ x^{2} -2x -15=0 \\ D=4+4*15=64 \\ x_{1} = \frac{2+8}{2}=5 \\ &#10;x_{2} = \frac{2-8}{2}=-3 \\ x^{2} -2x -15=(x-5)*(x+3)\ \textless \ 0 \\ &#10;x e \left(\\-3;5\right) \\ \left \{ {{x\ \textless \ 0} \atop {x e \left(\\-3;5\right)}} \right. \\ &#10;x e \left(\\-3;0\right)\\ S=-2+(-1)=-3&#10;
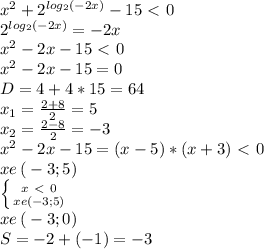
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
castlecrashers castlecrashers  19.07.2019 04:00
Решить пример: (a²+2b)(2a+b²). тема: умножение многочлена на многочлен....
liz93 liz93  19.07.2019 04:00
(1/4: 4+3/16)*(20целых5/8: 5целых1/2+1/4) напишите решение...
localhend localhend  19.07.2019 04:00
Решите уравнение : sin(+)=-1 sin(+)=-1...
cnejniyrayp08ixm cnejniyrayp08ixm  19.07.2019 04:00
Спростыть вираз: а) (5х+2у)^2 б) (-2-3a)^2 в) -(x+y)^2...
latypova04 latypova04  19.07.2019 04:00
Решить систему уравнений,! ! х/у + у/х = 5/2 х² + у² = 5...
kornilov1001 kornilov1001  19.07.2019 04:00
Решите систему неравенств в ответ запишите наименьшее целое решение....
Тирия Тирия  19.07.2019 04:00
Первые 200 км дороги из а в в автомобиль проехал с определенной скоростью,а остальные 150 км - со скоростью на 20 км/ч меньше.найдите начльную скорость,с которой ехал автомобиль,если...
Русик271 Русик271  26.06.2019 07:20
Составьте систему уравнений и решите : в шести больших и восьми маленьких коробках вместе 116 карандашей, а в трех больших и десяти маленьких – 118 карандашей. сколько карандашей...
daniil10457899Yb daniil10457899Yb  26.06.2019 07:20
Какое наименьшее значение может принимать выражение 9a^2+37-42a? а)12 б)-12 в)7 г)-7...
Саня11671873478 Саня11671873478  26.06.2019 07:20
Aквадрат -b квадрат / ab+bквадрат +b/a+b можно решения нужно...

Популярные вопросы