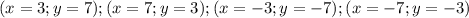Решить систему уравнений а) 3xy+y^2=-8 x-3y=10 б) x^2+y^2=58 xy=21
Другие вопросы по теме Алгебра
Популярные вопросы
- Переведи слово сочетания на язык 1)письмо маме. 2)конверты тайни. 3)сумка почтальона....
1 - Разложите на множители многочлен 25x²-10x+1-4y²...
3 - Определите в форме какого времени и лица даны глаголы на какой вопрос отвечают...
2 - Повесть булгакова м.а. собачье сердце ответите на вопросы ( в чем смысл финала?...
1 - 3). сколько граммов оксида магния можно получить при горении магния массой 2,4г?...
3 - Как составить звуковую схему слово предложение...
3 - Найти сопротивление второго проводника v=9в v=3в r1=12 ом...
3 - Сопротивление спирали электрического паяльника 500 ом,напряжение 220 в. найдите...
3 - Пуля массой 5г движется со скоростью v1= 200м/с и ударяется в куб массой 100г,...
1 - Перевести все в ары: 27 га,8 га,3 а,96000 м2 =2 это квадратных,9 км2,34 а. перевести...
2
ответ: нет решений
ответ: