Найти производную функции: f(x)=x+3/x-1
Ответы
Используем формулу дифференцирования частного
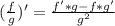
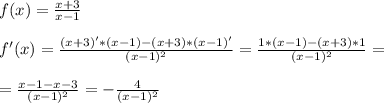
ПОКАЗАТЬ ОТВЕТЫ
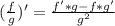
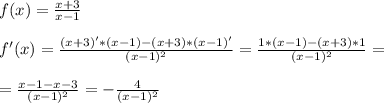
Другие вопросы по теме Алгебра
Популярные вопросы
- Write an email to Jack and answer the questions. Write 70–80 words....
2 - Бог охоты скотоводста у славян 1) Велес2)Ярило3) Стрибог4(Дажьбог...
3 - 2. Spell the words. 1. [ derlı)2. [ influəns]3. [ fræđail]4. [ tfeindsəbl]5....
1 - Постройте наклонный параллелепипед ABCDA1B1C1D1.Найдите центры граней...
2 - Привидите к стандартному виду и определите коэффициент одночлена...
1 - Онда турли елдердин саудагерлери аралас турғанын,ал қала тургындарынын...
2 - Знайдіть діагональ прямокутного паралелепіпеда за трьома його вимірами:...
3 - География 9 класс Контрольные вопросы Эндемик Антарктиды: а) волк...
2 - Используя карту плотности населения,расположи страны в порядке убывания...
3 - Напишите одно отличие монголоидной расы...
3