Решить, . буду .
 \geqslant 0)
Другие вопросы по теме Алгебра
Популярные вопросы
- Найти частное и остаток при деление. сделай проверку 81580: 9...
2 - Написать про головоногих ! 1)место обитания 2)симметрия тела 3)...
3 - Вставьте глагол в нужной форме это !...
2 - Почему в почве тундре таг же мало гумуса как и в пустыне...
1 - Придумайте и запишите фамилии,связанные с вашими делами,занятиями,играми.придуманные...
2 - Разновидностью соединительной ткани у человека не является: а)...
2 - Обьем прямоугольного параллепипеда 84 см.этот параллелепипеда...
3 - Взявшись за руки, шестеро детей образовали контур квадрата (стали...
3 - Порция пельменей в кафе пампушечка состоит из 18 пельменей. иван...
3 - Вкаком городе проходит основное действие трагедии у.шекспира ромео...
1
Метод рационализации: заменяем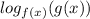 на
на 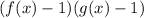 , учитывая ОДЗ .
, учитывая ОДЗ .