Найдите корни которые принадлежат интервалу , можно подробно показать отбор корней
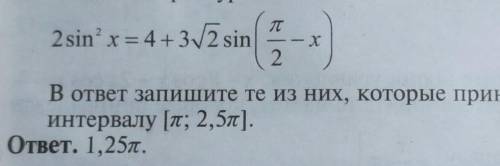
Другие вопросы по теме Алгебра
Популярные вопросы
- Найди периметр прямоугольника, у которогодлчнна одной стороны...
2 - На реакции с алюминием затрачено 109,5 г 10 процентной соляной...
2 - Как вы понимаете слова джона ива если желание сильно,мо иснальнение...
2 - Почему сначала надо удалить фон резьбы, а только потом выпилить...
3 - Почему в экваториальных областях изо дня в день идут дожди...
2 - Сколькими могут выбраны староста и физорг если каждый учащийся...
3 - Рассчитай расстояние от центра земли, на котором гравитационная...
2 - How would уоu тaке а fire in а very dark half ruined room? тhе...
2 - (1)full in the mising words/phrases: (shrugged, easy doing,...
2 - X+(1/(x-1)) полное исследование функции...
1
Здесь нет целых значений n , значит корней больше нет .
ответ : 1,25π
ответ: 1,25π
Объяснение: на фото