Найдите: a) область определения функции, заданной формулой:
1) y=9-2x
2) у=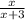
б) область значений функции у=
на отрезке -3<х<1

ЕСЛИ НЕ ЗНАЕТЕ НЕ ОТВЕЧАЙТЕ!! ИНАЧЕ АДМИНИСТРАТОРУ НА ВАС ЖАЛОБУ КИНУ

1) Для нахождения области определения функции y=9-2x нужно определить, в каких значениях переменная x является допустимой для подстановки в формулу. Область определения функции - это множество всех значений переменной x, для которых функция имеет смысл и определена.

В данном случае, функция является линейной, и мы можем подставить любое значение переменной x. Таким образом, область определения функции y=9-2x - это множество всех действительных чисел.

2) Для нахождения области определения функции у=?/(?+3) нужно определить, в каких значениях переменная x является допустимой для подстановки в формулу. Область определения функции - это множество всех значений переменной x, для которых функция имеет смысл и определена.

В данном случае, функция содержит дробь с переменной x в знаменателе. Чтобы избежать деления на ноль, нужно исключить значение x+3=0, что эквивалентно x=-3. Таким образом, область определения функции у=?/(?+3) - это множество всех действительных чисел, кроме x=-3.

б) Для нахождения области значений функции у=(3?+4)/7 на отрезке -3<х<1, нужно найти все возможные значения функции при изменении значения переменной x в указанном промежутке.

Мы можем пошагово решить данное уравнение, подставляя значения переменной x из заданного промежутка и вычисляя соответствующие значения функции.

1) Подставляем значение x=-3:
у=(3(-3)+4)/7=(-9+4)/7=-5/7

2) Подставляем значение x=-2:
у=(3(-2)+4)/7=(-6+4)/7=-2/7

3) Подставляем значение x=-1:
у=(3(-1)+4)/7=(-3+4)/7=1/7

4) Подставляем значение x=0:
у=(3(0)+4)/7=(0+4)/7=4/7

5) Подставляем значение x=1:
у=(3(1)+4)/7=(3+4)/7=7/7=1

Таким образом, область значений функции у=(3?+4)/7 на отрезке -3<х<1 - это множество всех возможных значений функции у при изменении значения переменной x в указанном промежутке. В данном случае, область значений функции у=(3?+4)/7 на отрезке -3<х<1 - это множество всех действительных чисел, кроме значения y=-5/7.

Надеюсь, данный ответ был понятен для школьника. Если у него возникнут дополнительные вопросы, он может задать их.