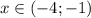Доброго времени суток, подскажите, . показательное неравенство с модулем.
Другие вопросы по теме Алгебра
Популярные вопросы
- Для экзамена заготовлено 20 билетов. Если студент на вытянутый...
3 - Задача по астрономии,решите...
2 - Неузгоджене означення НЕ ОБОВ ЯЗКОВО відокремлювати в реченні....
2 - Переведите предложения на английский язык, употребляя сложное...
2 - Переведите предложения на английский язык, употребляя сложное...
3 - 8. Знайдіть рядок, в якому ненаголошений голосний е при зміні...
2 - Аминокислоты. Белки Вариант 4 1. Агрегатное состояние аминокислот...
1 - Грамматический перевод 1. Новый банк построят? Деньги и специальные...
2 - Несогласный или инакомыслящий в период правления Брежнева назывался...
3 - Роман «Кысь», ответьте на во Почему Бенедикт становится санитаром?...
2
Т.к.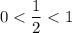 , то ф-я
, то ф-я 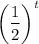 - убывающая, т.е. большему значению аргумента соответствует меньшее значение функции.
- убывающая, т.е. большему значению аргумента соответствует меньшее значение функции.
Значит, исходное неравенство равносильно
Случай первый:
Получим условие на раскрытие модуля со знаком "+"
Решим соответствующее неравенство
Получили пустое множество, значит, в этом первом случае неравенство решений не имеет.
Случай второй:
Получим условие на раскрытие модуля со знаком "-"
Решим соответствующее неравенство
Пересечём полученное множество с условием
ответ.