Делится ли (x+1) в шестой степени -x в шестой степени-2x-1 на (x-a)
Другие вопросы по теме Алгебра
Популярные вопросы
- Учесночниц в скелете нет а) ребер б)хрящей в)шейного отдела позвоночника...
2 - Банк выдал кредиты: на сумму 10 млн. руб. по ставке 20% годовых,...
2 - 150 : x - 15 = 8 решить уравнение . на...
2 - Сделайте фонетический разбор слова многосторонней, воспитанного,...
2 - √5*3²*√5*2в 4 степени найдите значение выражения....
3 - Для приготовления одной банки варенья нужно 4 кг ягод. сколько банок...
1 - Длина водохранилища на 200км больше его ширины. поездка на катере...
1 - Придумать 1 уравнение и решение с многозначными числами...
1 - Слинейки и циркуля начертить угол 15 градусов...
3 - Что полезного вы сделали для животных....
1
Разложим на множители многочлен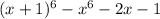
Т.е. многочлен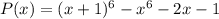 делится на
делится на  только при a = 0, a = -1 и a = -1/2
только при a = 0, a = -1 и a = -1/2