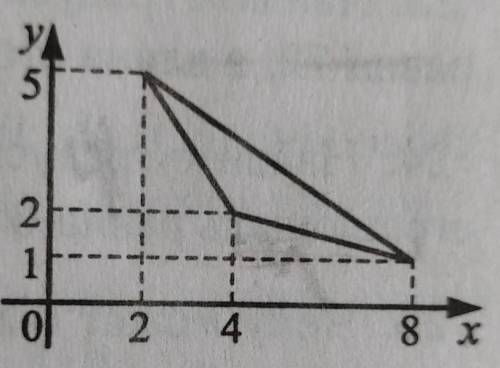
14. Найдите площадь треугольника, изображённого в координатной плоскости на данном справа рисунке.​

5

Объяснение:

этот треугольник входит в часть другого прямоуг. треугольника, площадь которого найти гораздо проще по формуле 1/2 ab, а потом вычесть из него другие кусочки

площадь прямоугольного треугольника= 1/2* 4*6=12

площадь искомого треугольника= 12-3-2-2=5

Чтобы найти площадь треугольника, нам нужно знать длины его сторон. Для этого мы можем использовать координаты вершин треугольника и формулу для расчета расстояния между двумя точками.

На рисунке видно, что вершины треугольника обозначены точками A(1,2), B(4,5) и C(2,6). Давайте найдем длины сторон треугольника.

Длина стороны AB:
Используем формулу для расчета расстояния между двумя точками:
AB = √((x2 - x1)^2 + (y2 - y1)^2)
AB = √((4 - 1)^2 + (5 - 2)^2)
AB = √(3^2 + 3^2)
AB = √(9 + 9)
AB = √18
AB ≈ 4.242

Длина стороны BC:
BC = √((x2 - x1)^2 + (y2 - y1)^2)
BC = √((2 - 4)^2 + (6 - 5)^2)
BC = √((-2)^2 + 1^2)
BC = √(4 + 1)
BC = √5
BC ≈ 2.236

Длина стороны AC:
AC = √((x2 - x1)^2 + (y2 - y1)^2)
AC = √((2 - 1)^2 + (6 - 2)^2)
AC = √(1^2 + 4^2)
AC = √(1 + 16)
AC = √17
AC ≈ 4.123

Теперь у нас есть длины всех трех сторон треугольника.
Для расчета площади треугольника, мы можем использовать формулу Герона:

S = √(p * (p - AB) * (p - BC) * (p - AC))

где p - полупериметр треугольника, который можно вычислить по формуле:

p = (AB + BC + AC) / 2

Подставим значения в формулы:

p = (4.242 + 2.236 + 4.123) / 2
p ≈ 5.801

S = √(5.801 * (5.801 - 4.242) * (5.801 - 2.236) * (5.801 - 4.123))
S = √(5.801 * 1.559 * 3.565 * 1.678)
S ≈ √(18.203)
S ≈ 4.269

Таким образом, площадь треугольника, изображенного на данный рисунке, примерно равна 4.269.