Ребят, можете с объяснением каждое уравнение
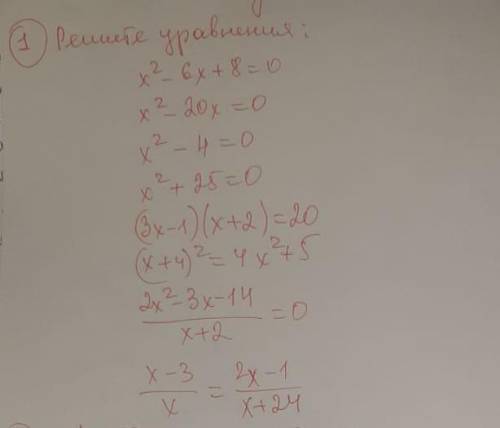
Другие вопросы по теме Русский язык
Популярные вопросы
- Як вы разумееце выраз нязводны род? - Пісьмянкоў. Продкі...
1 - Чаму кожны сямейны радавод нагадвае дрэва, а людская супольнасць падобная...
2 - Якой паўстае зямля Беларусі ва ўяўленні паэта? Якія малюнкі і вобразы...
2 - Ці можам мы назваць людзей, якія жывуць на нашай Зямлі, вялікай сям’ёй?...
1 - У адным з твораў паэт Максім Танк зазначае, што сёння мы маем ад Скарыны-бацькі...
2 - Якімі вобразамі звязана ўяўленне паэтэсы пра радзіму? - Лось. Продкі...
2 - Разгледзьце рэпрадукцыю карціны Эдуарда Белагурава “Партрэт бацькоў”....
1 - Што гаворыць паэт пра сваіх продкаў? - Пісьмянкоў. Продкі...
2 - Разгледзьце фрагмент роспісу Эдуарда Рымаровіча «Дзяцінства». (Гл. уклейку.)...
3 - Якое прызначэнне мастацкай кнігі? У чым вам бачыцца яе каштоўнасць?...
2
Для того, чтобы найти решение x2 - 6x + 8 = 0 полного квадратного уравнения мы применим мы начнем с нахождения дискриминанта.
Для его нахождения мы выпишем коэффициенты этого уравнения:
a = 1; b = -6; c = 8.
Вспомним и применим формулу для нахождения дискриминанта:
D = b2 - 4ac = (-6)2 - 4 * 1 * 8 = 36 - 32 = 4.
Корни уравнения мы будем искать по следующим формулам:
x1 = (-b + √D)/2a = (6 + √4)/2 * 1 = (6 + 2)/2 = 8/2 = 4;
x2 = (-b - √D)/2a = (6 - √4)/2 * 1 = (6 - 2)/2 = 4/2 = 2;
ответ: x = 4; x = 2.